Simulation of diffusion networks: rdiffnet
Thomas W. Valente and George G. Vega Yon
Introduction
Before we start, a review of the concepts we will be using here
- Exposure: Proportion/number of neighbors that has adopted an innovation at each point in time.
- Threshold: The proportion/number of your neighbors who had adopted at or one time period before ego (the focal individual) adopted.
- Infectiousness: How much \(i\)’s adoption affects her alters.
- Susceptibility: How much \(i\)’s alters’ adoption affects her.
- Structural equivalence: How similar are \(i\) and \(j\) in terms of position in the network.
Simulating diffusion networks
We will simulate a diffusion network with the following parameters:
- Will have 1,000 vertices,
- Will span 20 time periods,
- The initial adopters (seeds) will be selected random,
- Seeds will be a 10% of the network,
- The graph (network) will be small-world,
- Will use the WS algorithmwith \(p=.2\) (probability of rewire).
- Threshold levels will be uniformly distributed between [0.3, 0.7]
To generate this diffusion network we can use the rdiffnet function included in the package:
# Setting the seed for the RNG
set.seed(1213)
# Generating a random diffusion network
net <- rdiffnet(
n = 1e3, # 1.
t = 20, # 2.
seed.nodes = "random", # 3.
seed.p.adopt = .1, # 4.
seed.graph = "small-world", # 5.
rgraph.args = list(p=.2), # 6.
threshold.dist = function(x) runif(1, .3, .7) # 7.
)The function
rdiffnetgenerates random diffusion networks. Main features:Simulating random graph or using your own,
Setting threshold levels per node,
Network rewiring throughout the simulation, and
Setting the seed nodes.
The simulation algorithm is as follows:
If required, a baseline graph is created,
Set of initial adopters and threshold distribution are established,
The set of t networks is created (if required), and
Simulation starts at t=2, assigning adopters based on exposures and thresholds:
For each \(i \in N\), if its exposure at \(t-1\) is greater than its threshold, then adopts, otherwise continue without change.
next \(i\)
Rumor spreading
library(netdiffuseR)
set.seed(09)
diffnet_rumor <- rdiffnet(
n = 5e2,
t = 5,
seed.graph = "small-world",
rgraph.args = list(k = 4, p = .3),
seed.nodes = "random",
seed.p.adopt = .05,
rewire = TRUE,
threshold.dist = function(i) 1L,
exposure.args = list(normalized = FALSE)
)summary(diffnet_rumor)# Diffusion network summary statistics
# Name : A diffusion network
# Behavior : Random contagion
# -----------------------------------------------------------------------------
# Period Adopters Cum Adopt. (%) Hazard Rate Density Moran's I (sd)
# -------- ---------- ---------------- ------------- --------- ----------------
# 1 25 25 (0.05) - 0.01 -0.00 (0.00)
# 2 78 103 (0.21) 0.16 0.01 0.01 (0.00) ***
# 3 187 290 (0.58) 0.47 0.01 0.01 (0.00) ***
# 4 183 473 (0.95) 0.87 0.01 0.01 (0.00) ***
# 5 27 500 (1.00) 1.00 0.01 -
# -----------------------------------------------------------------------------
# Left censoring : 0.05 (25)
# Right centoring : 0.00 (0)
# # of nodes : 500
#
# Moran's I was computed on contemporaneous autocorrelation using 1/geodesic
# values. Significane levels *** <= .01, ** <= .05, * <= .1.plot_diffnet(diffnet_rumor, slices = c(1, 3, 5))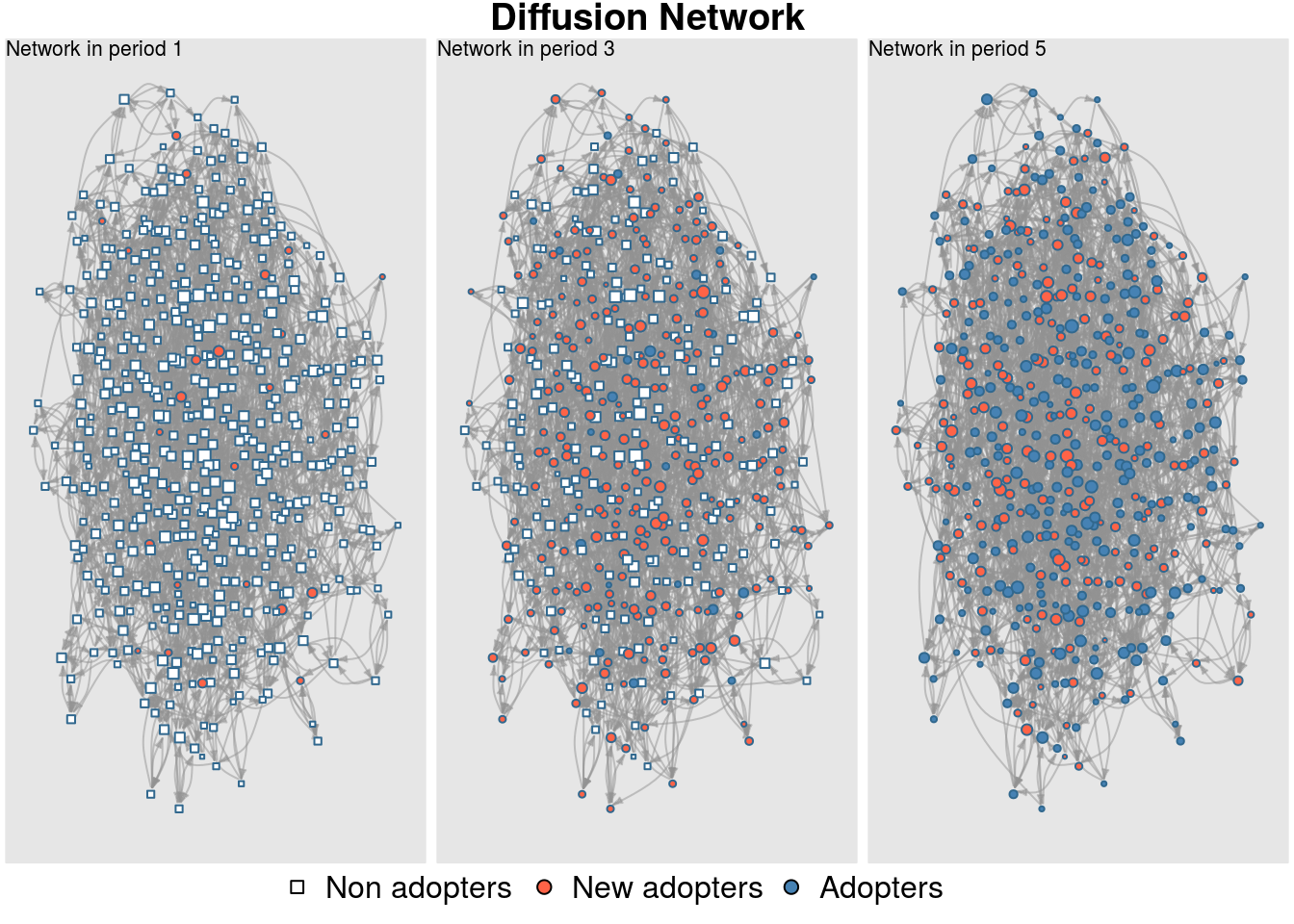
# We want to use igraph to compute layout
igdf <- diffnet_to_igraph(diffnet_rumor, slices=c(1,2))[[1]]
pos <- igraph::layout_with_drl(igdf)
plot_diffnet2(diffnet_rumor, vertex.size = dgr(diffnet_rumor)[,1], layout=pos)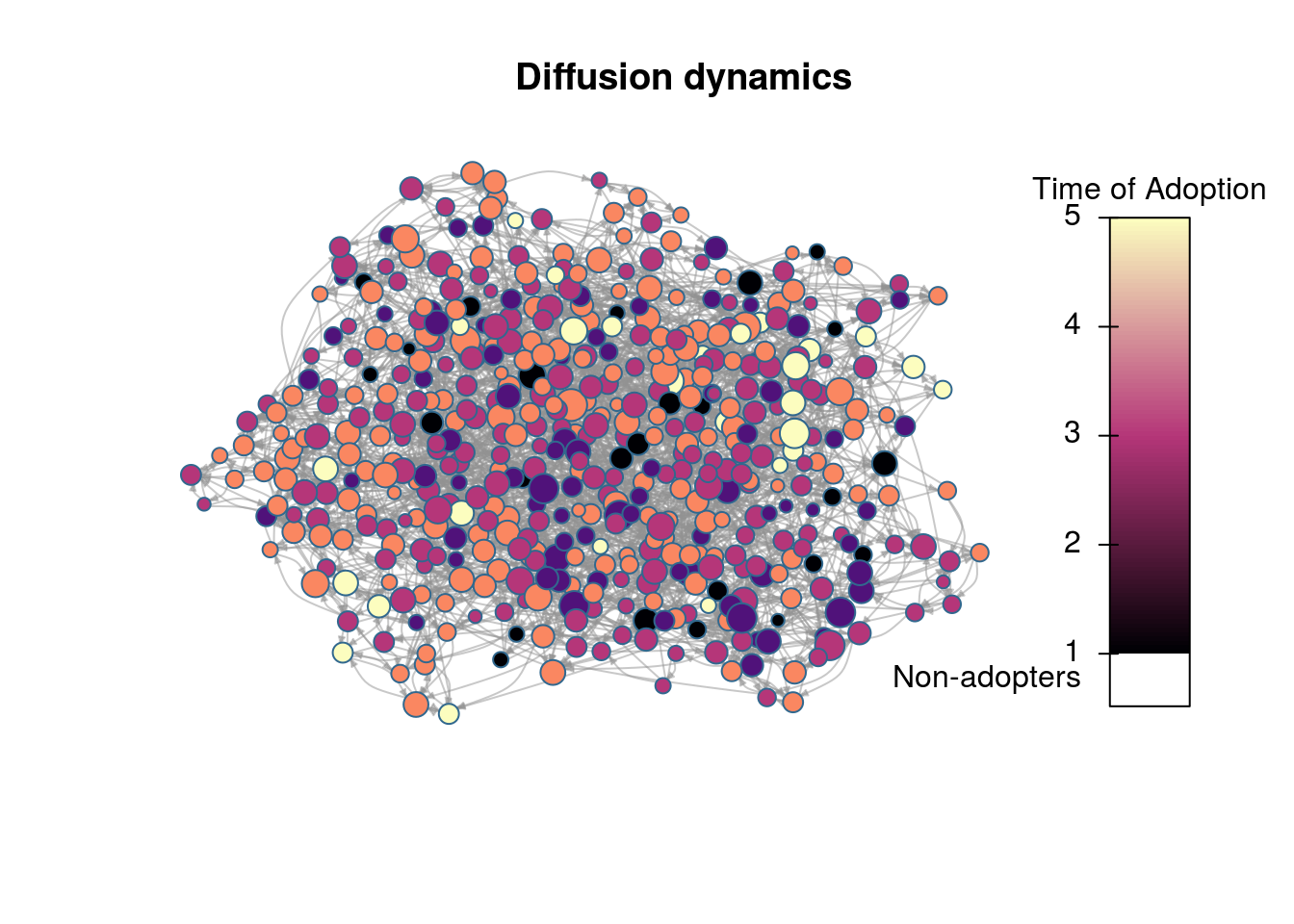
Difussion
set.seed(09)
diffnet_complex <- rdiffnet(
seed.graph = diffnet_rumor$graph,
seed.nodes = which(diffnet_rumor$toa == 1),
rewire = FALSE,
threshold.dist = function(i) rbeta(1, 3, 10),
name = "Diffusion",
behavior = "Some social behavior"
)plot_adopters(diffnet_rumor, what = "cumadopt", include.legend = FALSE)
plot_adopters(diffnet_complex, bg="tomato", add=TRUE, what = "cumadopt")
legend("topleft", legend = c("Disease", "Complex"), col = c("lightblue", "tomato"),
bty = "n", pch=19)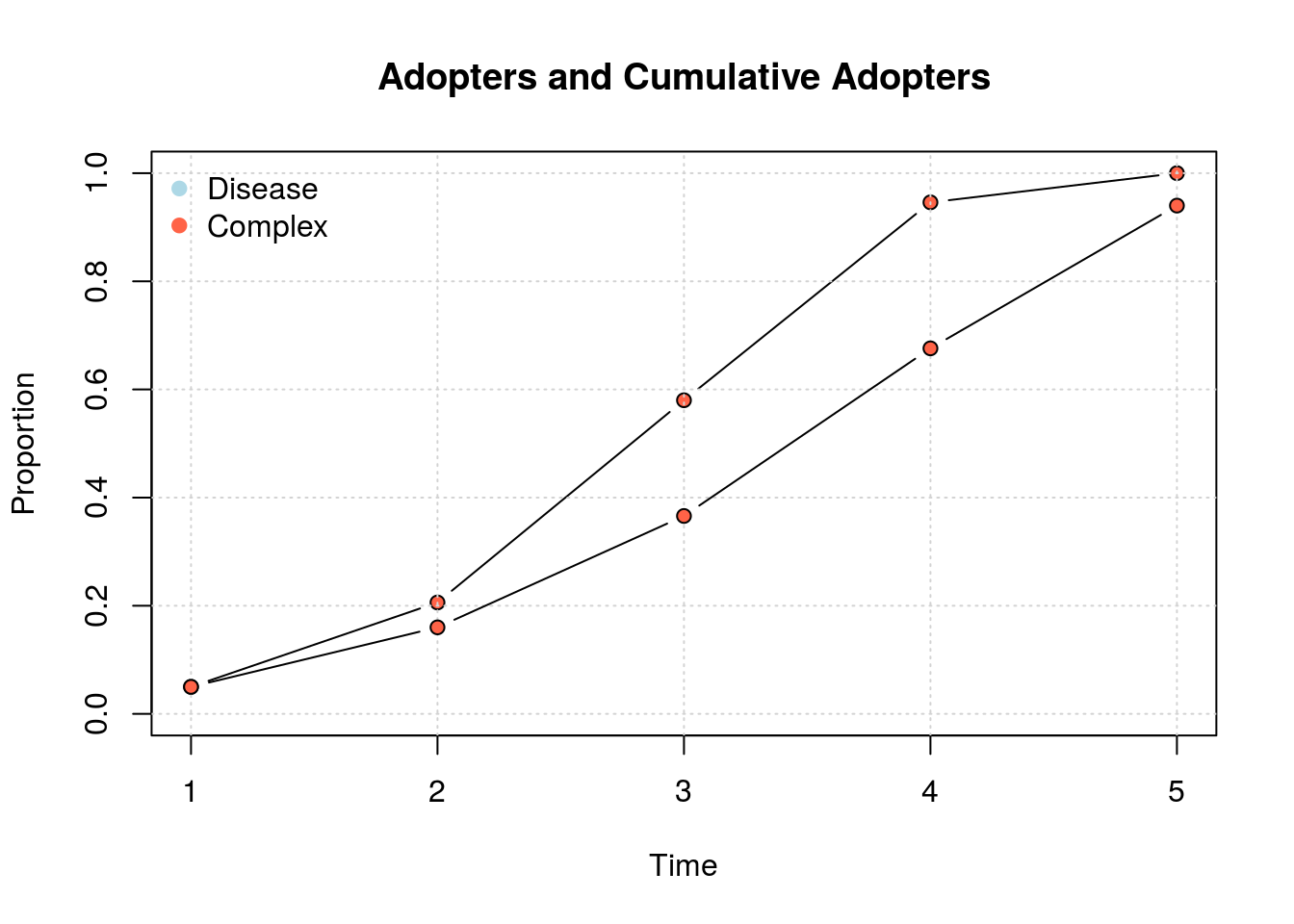
Mentor Matching
# Finding mentors
mentors <- mentor_matching(diffnet_rumor, 25, lead.ties.method = "random")
# Simulating diffusion with these mentors
set.seed(09)
diffnet_mentored <- rdiffnet(
seed.graph = diffnet_complex,
seed.nodes = which(mentors$`1`$isleader),
rewire = FALSE,
threshold.dist = diffnet_complex[["real_threshold"]],
name = "Diffusion using Mentors"
)
summary(diffnet_mentored)# Diffusion network summary statistics
# Name : Diffusion using Mentors
# Behavior : Random contagion
# -----------------------------------------------------------------------------
# Period Adopters Cum Adopt. (%) Hazard Rate Density Moran's I (sd)
# -------- ---------- ---------------- ------------- --------- ----------------
# 1 25 25 (0.05) - 0.01 -0.00 (0.00)
# 2 92 117 (0.23) 0.19 0.01 0.01 (0.00) ***
# 3 152 269 (0.54) 0.40 0.01 0.01 (0.00) ***
# 4 150 419 (0.84) 0.65 0.01 0.01 (0.00) ***
# 5 73 492 (0.98) 0.90 0.01 -0.00 (0.00) **
# -----------------------------------------------------------------------------
# Left censoring : 0.05 (25)
# Right centoring : 0.02 (8)
# # of nodes : 500
#
# Moran's I was computed on contemporaneous autocorrelation using 1/geodesic
# values. Significane levels *** <= .01, ** <= .05, * <= .1.cumulative_adopt_count(diffnet_complex)# 1 2 3 4 5
# num 25.00 80.00 183.0000 338.0000000 470.0000000
# prop 0.05 0.16 0.3660 0.6760000 0.9400000
# rate 0.00 2.20 1.2875 0.8469945 0.3905325cumulative_adopt_count(diffnet_mentored)# 1 2 3 4 5
# num 25.00 117.000 269.000000 419.0000000 492.0000000
# prop 0.05 0.234 0.538000 0.8380000 0.9840000
# rate 0.00 3.680 1.299145 0.5576208 0.1742243Example by changing threshold
# Simulating a scale-free homophilic network
set.seed(1231)
X <- rep(c(1,1,1,1,1,0,0,0,0,0), 50)
net <- rgraph_ba(t = 499, m=4, eta = X)
# Taking a look in igraph
ig <- igraph::graph_from_adjacency_matrix(net)
plot(ig, vertex.color = c("azure", "tomato")[X+1], vertex.label = NA,
vertex.size = sqrt(dgr(net)))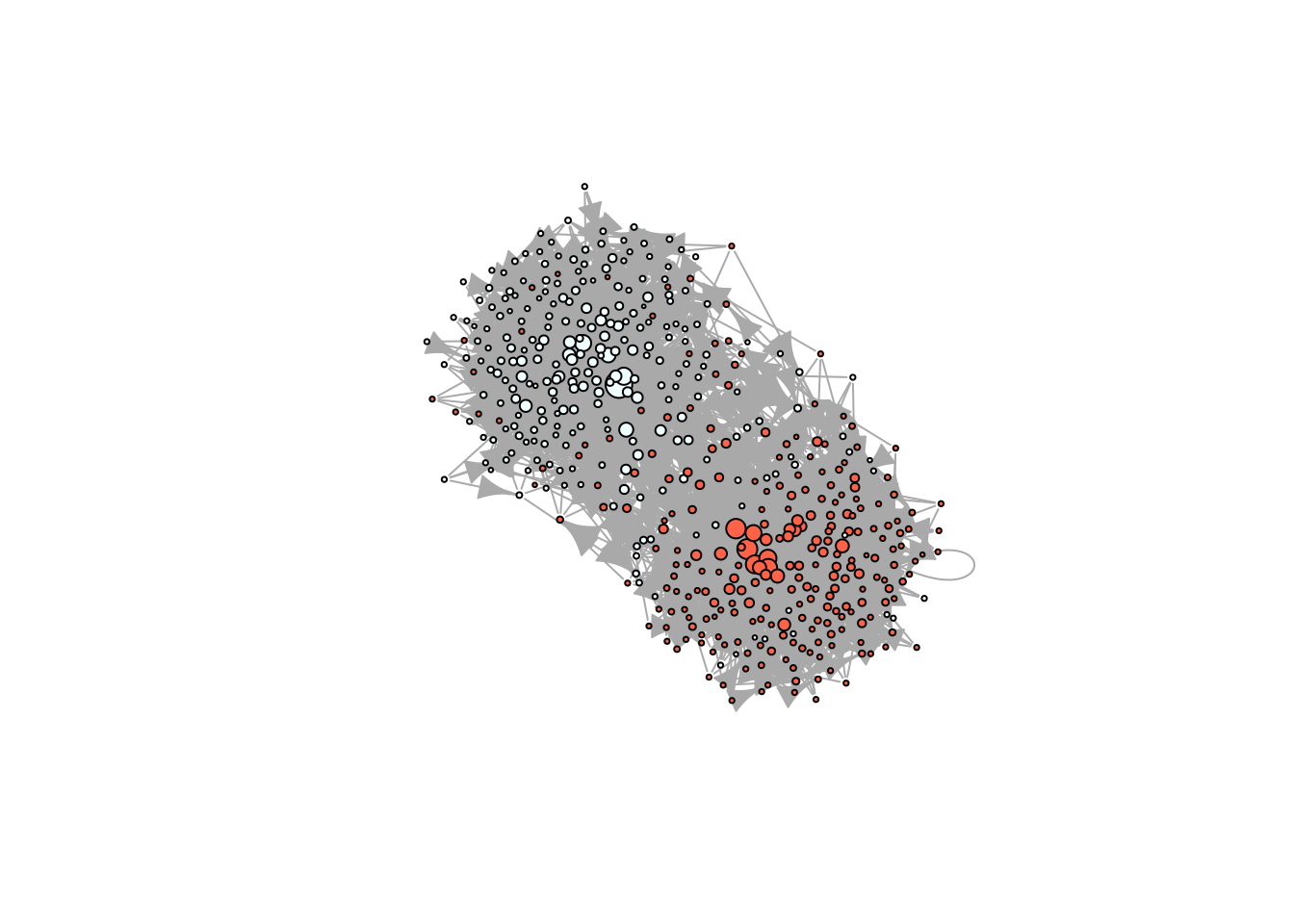
# Now, simulating a bunch of diffusion processes
nsim <- 500L
ans_1and2 <- vector("list", nsim)
set.seed(223)
for (i in 1:nsim) {
# We just want the cum adopt count
ans_1and2[[i]] <-
cumulative_adopt_count(
rdiffnet(
seed.graph = net,
t = 10,
threshold.dist = sample(1:2, 500L, TRUE),
seed.nodes = "random",
seed.p.adopt = .10,
exposure.args = list(outgoing = FALSE, normalized = FALSE),
rewire = FALSE
)
)
# Are we there yet?
if (!(i %% 50))
message("Simulation ", i," of ", nsim, " done.")
}
# Simulation 50 of 500 done.
# Simulation 100 of 500 done.
# Simulation 150 of 500 done.
# Simulation 200 of 500 done.
# Simulation 250 of 500 done.
# Simulation 300 of 500 done.
# Simulation 350 of 500 done.
# Simulation 400 of 500 done.
# Simulation 450 of 500 done.
# Simulation 500 of 500 done.
# Extracting prop
ans_1and2 <- do.call(rbind, lapply(ans_1and2, "[", i="prop", j=))
ans_2and3 <- vector("list", nsim)
set.seed(223)
for (i in 1:nsim) {
# We just want the cum adopt count
ans_2and3[[i]] <-
cumulative_adopt_count(
rdiffnet(
seed.graph = net,
t = 10,
threshold.dist = sample(2:3, 500L, TRUE),
seed.nodes = "random",
seed.p.adopt = .10,
exposure.args = list(outgoing = FALSE, normalized = FALSE),
rewire = FALSE
)
)
# Are we there yet?
if (!(i %% 50))
message("Simulation ", i," of ", nsim, " done.")
}
# Simulation 50 of 500 done.
# Simulation 100 of 500 done.
# Simulation 150 of 500 done.
# Simulation 200 of 500 done.
# Simulation 250 of 500 done.
# Simulation 300 of 500 done.
# Simulation 350 of 500 done.
# Simulation 400 of 500 done.
# Simulation 450 of 500 done.
# Simulation 500 of 500 done.
ans_2and3 <- do.call(rbind, lapply(ans_2and3, "[", i="prop", j=))This can actually be simplified by using the function rdiffnet_multiple. The following lines of code accomplish the same as the previous code avoiding the for-loop (from the user’s perspective). Besides of the usual parameters passed to rdiffnet, the rdiffnet_multiple function requires R (number of repetitions/simulations), and statistic (a function that returns the statistic of insterst). Optionally, the user may choose to specify the number of clusters to run it in parallel (multiple CPUs):
ans_1and3 <- rdiffnet_multiple(
# Num of sim
R = nsim,
# Statistic
statistic = function(d) cumulative_adopt_count(d)["prop",],
seed.graph = net,
t = 10,
threshold.dist = sample(1:3, 500, TRUE),
seed.nodes = "random",
seed.p.adopt = .1,
rewire = FALSE,
exposure.args = list(outgoing=FALSE, normalized=FALSE),
# Running on 4 cores
ncpus = 4L
)boxplot(ans_1and2, col="ivory", xlab = "Time", ylab = "Threshold")
boxplot(ans_2and3, col="tomato", add=TRUE)
boxplot(t(ans_1and3), col = "steelblue", add=TRUE)
legend(
"topleft",
fill = c("ivory", "tomato", "steelblue"),
legend = c("1/2", "2/3", "1/3"),
title = "Threshold range",
bty ="n"
)
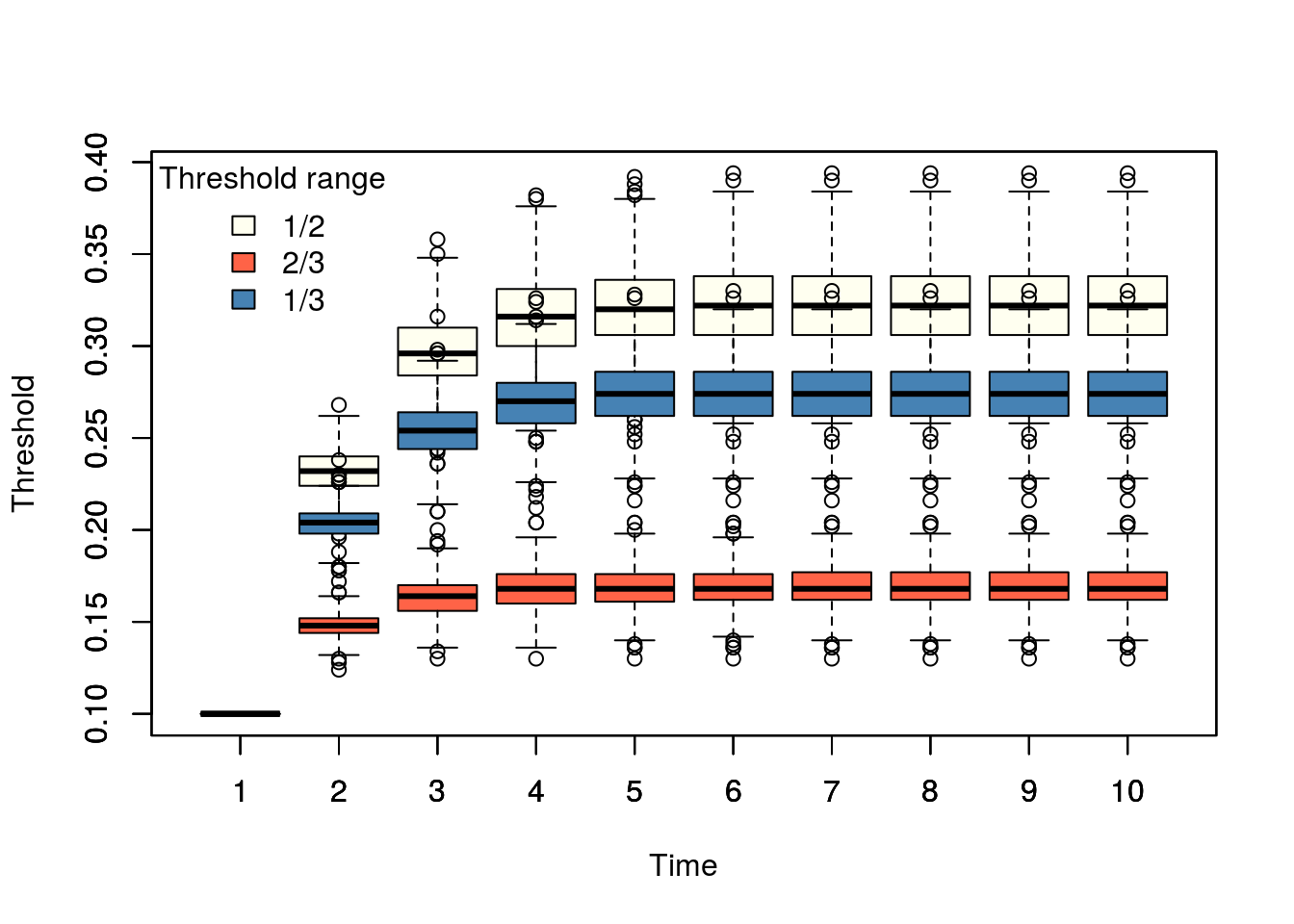
- Example simulating a thousand networks by changing threshold levels. The final prevalence, or hazard as a function of threshold levels.
Problems
- Given the following types of networks: Small-world, Scale-free, Bernoulli, what set of \(n\) initiators maximizes diffusion? (solution script and solution plot)
LS0tCnRpdGxlOiAiU2ltdWxhdGlvbiBvZiBkaWZmdXNpb24gbmV0d29ya3M6IHJkaWZmbmV0IgphdXRob3I6ICJUaG9tYXMgVy4gVmFsZW50ZSBhbmQgR2VvcmdlIEcuIFZlZ2EgWW9uIgotLS0KCmBgYHtyIHNldHVwLCBlY2hvPUZBTFNFLCBtZXNzYWdlPUZBTFNFLCB3YXJuaW5nPUZBTFNFfQpsaWJyYXJ5KG5ldGRpZmZ1c2VSKQprbml0cjo6b3B0c19jaHVuayRzZXQoY29tbWVudCA9ICIjIikKCmBgYAoKIyBJbnRyb2R1Y3Rpb24KCkJlZm9yZSB3ZSBzdGFydCwgYSByZXZpZXcgb2YgdGhlIGNvbmNlcHRzIHdlIHdpbGwgYmUgdXNpbmcgaGVyZQoKMS4gRXhwb3N1cmU6IFByb3BvcnRpb24vbnVtYmVyIG9mIG5laWdoYm9ycyB0aGF0IGhhcyBhZG9wdGVkIGFuIGlubm92YXRpb24gYXQgZWFjaCBwb2ludCBpbiB0aW1lLgoyLiBUaHJlc2hvbGQ6IFRoZSBwcm9wb3J0aW9uL251bWJlciBvZiB5b3VyIG5laWdoYm9ycyB3aG8gaGFkIGFkb3B0ZWQgYXQgb3Igb25lIHRpbWUgcGVyaW9kIGJlZm9yZSBlZ28gKHRoZSBmb2NhbCBpbmRpdmlkdWFsKSBhZG9wdGVkLgozLiBJbmZlY3Rpb3VzbmVzczogSG93IG11Y2ggJGkkJ3MgYWRvcHRpb24gYWZmZWN0cyBoZXIgYWx0ZXJzLgo0LiBTdXNjZXB0aWJpbGl0eTogSG93IG11Y2ggJGkkJ3MgYWx0ZXJzJyBhZG9wdGlvbiBhZmZlY3RzIGhlci4KNS4gU3RydWN0dXJhbCBlcXVpdmFsZW5jZTogSG93IHNpbWlsYXIgYXJlICRpJCBhbmQgJGokIGluIHRlcm1zIG9mIHBvc2l0aW9uIGluIHRoZSBuZXR3b3JrLgoKIyBTaW11bGF0aW5nIGRpZmZ1c2lvbiBuZXR3b3JrcwoKV2Ugd2lsbCBzaW11bGF0ZSBhIGRpZmZ1c2lvbiBuZXR3b3JrIHdpdGggdGhlIGZvbGxvd2luZyBwYXJhbWV0ZXJzOgoKMS4gIFdpbGwgaGF2ZSAxLDAwMCB2ZXJ0aWNlcywKMi4gIFdpbGwgc3BhbiAyMCB0aW1lIHBlcmlvZHMsCjMuICBUaGUgaW5pdGlhbCBhZG9wdGVycyAoc2VlZHMpIHdpbGwgYmUgc2VsZWN0ZWQgcmFuZG9tLAo0LiAgU2VlZHMgd2lsbCBiZSBhIDEwXCUgb2YgdGhlIG5ldHdvcmssCjUuICBUaGUgZ3JhcGggKG5ldHdvcmspIHdpbGwgYmUgc21hbGwtd29ybGQsCjYuICBXaWxsIHVzZSB0aGUgV1MgYWxnb3JpdGhtd2l0aCAkcD0uMiQgKHByb2JhYmlsaXR5IG9mIHJld2lyZSkuCjcuICBUaHJlc2hvbGQgbGV2ZWxzIHdpbGwgYmUgdW5pZm9ybWx5IGRpc3RyaWJ1dGVkIGJldHdlZW4gWzAuMywgMC43XF0KClRvIGdlbmVyYXRlIHRoaXMgZGlmZnVzaW9uIG5ldHdvcmsgd2UgY2FuIHVzZSB0aGUgYHJkaWZmbmV0YCBmdW5jdGlvbiBpbmNsdWRlZCBpbiB0aGUgcGFja2FnZToKCgpgYGB7ciBHZW5lcmF0aW5nIHRoZSByYW5kb20gZ3JhcGh9CiMgU2V0dGluZyB0aGUgc2VlZCBmb3IgdGhlIFJORwpzZXQuc2VlZCgxMjEzKQoKIyBHZW5lcmF0aW5nIGEgcmFuZG9tIGRpZmZ1c2lvbiBuZXR3b3JrCm5ldCA8LSByZGlmZm5ldCgKICBuICAgICAgICAgICAgICA9IDFlMywgICAgICAgICAgICAgICAgICAgICAgICAgIyAxLgogIHQgICAgICAgICAgICAgID0gMjAsICAgICAgICAgICAgICAgICAgICAgICAgICAjIDIuCiAgc2VlZC5ub2RlcyAgICAgPSAicmFuZG9tIiwgICAgICAgICAgICAgICAgICAgICMgMy4KICBzZWVkLnAuYWRvcHQgICA9IC4xLCAgICAgICAgICAgICAgICAgICAgICAgICAgIyA0LgogIHNlZWQuZ3JhcGggICAgID0gInNtYWxsLXdvcmxkIiwgICAgICAgICAgICAgICAjIDUuCiAgcmdyYXBoLmFyZ3MgICAgPSBsaXN0KHA9LjIpLCAgICAgICAgICAgICAgICAgICMgNi4KICB0aHJlc2hvbGQuZGlzdCA9IGZ1bmN0aW9uKHgpIHJ1bmlmKDEsIC4zLCAuNykgIyA3LgogICkKYGBgCgoKKiAgIFRoZSBmdW5jdGlvbiBgcmRpZmZuZXRgIGdlbmVyYXRlcyByYW5kb20gZGlmZnVzaW9uIG5ldHdvcmtzLiBNYWluIGZlYXR1cmVzOgogICAgCiAgICAxLiAgU2ltdWxhdGluZyByYW5kb20gZ3JhcGggb3IgdXNpbmcgeW91ciBvd24sCiAgICAKICAgIDIuICBTZXR0aW5nIHRocmVzaG9sZCBsZXZlbHMgcGVyIG5vZGUsCiAgICAKICAgIDMuICBOZXR3b3JrIHJld2lyaW5nIHRocm91Z2hvdXQgdGhlIHNpbXVsYXRpb24sIGFuZAogICAgCiAgICA0LiAgU2V0dGluZyB0aGUgc2VlZCBub2Rlcy4KICAgIAogICAgCiogICBUaGUgc2ltdWxhdGlvbiBhbGdvcml0aG0gaXMgYXMgZm9sbG93czoKICAgIAogICAgMS4gIElmIHJlcXVpcmVkLCBhIGJhc2VsaW5lIGdyYXBoIGlzIGNyZWF0ZWQsCiAgICAKICAgIDIuICBTZXQgb2YgaW5pdGlhbCBhZG9wdGVycyBhbmQgdGhyZXNob2xkIGRpc3RyaWJ1dGlvbiBhcmUgZXN0YWJsaXNoZWQsCiAgICAKICAgIDMuICBUaGUgc2V0IG9mIHQgbmV0d29ya3MgaXMgY3JlYXRlZCAoaWYgcmVxdWlyZWQpLCBhbmQKICAgIAogICAgNC4gIFNpbXVsYXRpb24gc3RhcnRzIGF0IHQ9MiwgYXNzaWduaW5nIGFkb3B0ZXJzIGJhc2VkIG9uIGV4cG9zdXJlcyBhbmQgdGhyZXNob2xkczoKICAgIAogICAgICAgIGEuICBGb3IgZWFjaCAkaSBcaW4gTiQsIGlmIGl0cyBleHBvc3VyZSBhdCAkdC0xJCBpcyBncmVhdGVyIHRoYW4gaXRzIHRocmVzaG9sZCwgdGhlbiAKICAgICAgICAgICAgYWRvcHRzLCBvdGhlcndpc2UgY29udGludWUgd2l0aG91dCBjaGFuZ2UuCiAgICAgICAgICAgIAogICAgICAgIGIuICBuZXh0ICRpJAogICAgCiMgUnVtb3Igc3ByZWFkaW5nCgpgYGB7ciBzaW0tcnVtb3J9CmxpYnJhcnkobmV0ZGlmZnVzZVIpCgpzZXQuc2VlZCgwOSkKZGlmZm5ldF9ydW1vciA8LSByZGlmZm5ldCgKICBuID0gNWUyLAogIHQgPSA1LCAKICBzZWVkLmdyYXBoID0gInNtYWxsLXdvcmxkIiwKICByZ3JhcGguYXJncyA9IGxpc3QoayA9IDQsIHAgPSAuMyksCiAgc2VlZC5ub2RlcyA9ICJyYW5kb20iLAogIHNlZWQucC5hZG9wdCA9IC4wNSwKICByZXdpcmUgPSBUUlVFLAogIHRocmVzaG9sZC5kaXN0ID0gZnVuY3Rpb24oaSkgMUwsCiAgZXhwb3N1cmUuYXJncyA9IGxpc3Qobm9ybWFsaXplZCA9IEZBTFNFKQogICkKYGBgCgpgYGB7ciBzdW1tYXJ5LXJ1bW9yfQpzdW1tYXJ5KGRpZmZuZXRfcnVtb3IpCmBgYAoKCmBgYHtyIHBsb3QtcnVtb3IsIGZpZy5hbGlnbj0nY2VudGVyJywgY2FjaGU9VFJVRX0KcGxvdF9kaWZmbmV0KGRpZmZuZXRfcnVtb3IsIHNsaWNlcyA9IGMoMSwgMywgNSkpCgojIFdlIHdhbnQgdG8gdXNlIGlncmFwaCB0byBjb21wdXRlIGxheW91dAppZ2RmIDwtIGRpZmZuZXRfdG9faWdyYXBoKGRpZmZuZXRfcnVtb3IsIHNsaWNlcz1jKDEsMikpW1sxXV0KcG9zIDwtIGlncmFwaDo6bGF5b3V0X3dpdGhfZHJsKGlnZGYpCgpwbG90X2RpZmZuZXQyKGRpZmZuZXRfcnVtb3IsIHZlcnRleC5zaXplID0gZGdyKGRpZmZuZXRfcnVtb3IpWywxXSwgbGF5b3V0PXBvcykKYGBgCgoKIyBEaWZ1c3Npb24KCmBgYHtyIHNpbS1jb21wbGV4fQpzZXQuc2VlZCgwOSkKZGlmZm5ldF9jb21wbGV4IDwtIHJkaWZmbmV0KAogIHNlZWQuZ3JhcGggPSBkaWZmbmV0X3J1bW9yJGdyYXBoLAogIHNlZWQubm9kZXMgPSB3aGljaChkaWZmbmV0X3J1bW9yJHRvYSA9PSAxKSwKICByZXdpcmUgPSBGQUxTRSwKICB0aHJlc2hvbGQuZGlzdCA9IGZ1bmN0aW9uKGkpIHJiZXRhKDEsIDMsIDEwKSwKICBuYW1lID0gIkRpZmZ1c2lvbiIsCiAgYmVoYXZpb3IgPSAiU29tZSBzb2NpYWwgYmVoYXZpb3IiCikKCmBgYAoKYGBge3IgcGxvdC1jb21wbGV4LWFuZC1kaXNlYXNlfQpwbG90X2Fkb3B0ZXJzKGRpZmZuZXRfcnVtb3IsIHdoYXQgPSAiY3VtYWRvcHQiLCBpbmNsdWRlLmxlZ2VuZCA9IEZBTFNFKQpwbG90X2Fkb3B0ZXJzKGRpZmZuZXRfY29tcGxleCwgYmc9InRvbWF0byIsIGFkZD1UUlVFLCB3aGF0ID0gImN1bWFkb3B0IikKbGVnZW5kKCJ0b3BsZWZ0IiwgbGVnZW5kID0gYygiRGlzZWFzZSIsICJDb21wbGV4IiksIGNvbCA9IGMoImxpZ2h0Ymx1ZSIsICJ0b21hdG8iKSwKICAgICAgIGJ0eSA9ICJuIiwgcGNoPTE5KQpgYGAKCgojIE1lbnRvciBNYXRjaGluZwoKYGBge3IgbWVudG9yLW1hdGNoLCBjYWNoZSA9IFRSVUV9CgojIEZpbmRpbmcgbWVudG9ycwptZW50b3JzIDwtIG1lbnRvcl9tYXRjaGluZyhkaWZmbmV0X3J1bW9yLCAyNSwgbGVhZC50aWVzLm1ldGhvZCA9ICJyYW5kb20iKQoKIyBTaW11bGF0aW5nIGRpZmZ1c2lvbiB3aXRoIHRoZXNlIG1lbnRvcnMKc2V0LnNlZWQoMDkpCmRpZmZuZXRfbWVudG9yZWQgPC0gcmRpZmZuZXQoCiAgc2VlZC5ncmFwaCA9IGRpZmZuZXRfY29tcGxleCwKICBzZWVkLm5vZGVzID0gd2hpY2gobWVudG9ycyRgMWAkaXNsZWFkZXIpLAogIHJld2lyZSA9IEZBTFNFLAogIHRocmVzaG9sZC5kaXN0ID0gZGlmZm5ldF9jb21wbGV4W1sicmVhbF90aHJlc2hvbGQiXV0sCiAgbmFtZSA9ICJEaWZmdXNpb24gdXNpbmcgTWVudG9ycyIKKQoKc3VtbWFyeShkaWZmbmV0X21lbnRvcmVkKQpgYGAKCmBgYHtyIHRvYV9tYXQtbWVudG9yc30KY3VtdWxhdGl2ZV9hZG9wdF9jb3VudChkaWZmbmV0X2NvbXBsZXgpCmN1bXVsYXRpdmVfYWRvcHRfY291bnQoZGlmZm5ldF9tZW50b3JlZCkKYGBgCgoKIyBFeGFtcGxlIGJ5IGNoYW5naW5nIHRocmVzaG9sZAoKYGBge3Igc2ltLXNpbSwgY2FjaGUgPSBUUlVFLCBjb2xsYXBzZSA9IFRSVUV9CgojIFNpbXVsYXRpbmcgYSBzY2FsZS1mcmVlIGhvbW9waGlsaWMgbmV0d29yawpzZXQuc2VlZCgxMjMxKQpYIDwtIHJlcChjKDEsMSwxLDEsMSwwLDAsMCwwLDApLCA1MCkKbmV0IDwtIHJncmFwaF9iYSh0ID0gNDk5LCBtPTQsIGV0YSA9IFgpCgojIFRha2luZyBhIGxvb2sgaW4gaWdyYXBoCmlnICA8LSBpZ3JhcGg6OmdyYXBoX2Zyb21fYWRqYWNlbmN5X21hdHJpeChuZXQpCnBsb3QoaWcsIHZlcnRleC5jb2xvciA9IGMoImF6dXJlIiwgInRvbWF0byIpW1grMV0sIHZlcnRleC5sYWJlbCA9IE5BLAogICAgIHZlcnRleC5zaXplID0gc3FydChkZ3IobmV0KSkpCgojIE5vdywgc2ltdWxhdGluZyBhIGJ1bmNoIG9mIGRpZmZ1c2lvbiBwcm9jZXNzZXMKbnNpbSA8LSA1MDBMCmFuc18xYW5kMiA8LSB2ZWN0b3IoImxpc3QiLCBuc2ltKQpzZXQuc2VlZCgyMjMpCmZvciAoaSBpbiAxOm5zaW0pIHsKICAjIFdlIGp1c3Qgd2FudCB0aGUgY3VtIGFkb3B0IGNvdW50CiAgYW5zXzFhbmQyW1tpXV0gPC0gCiAgICBjdW11bGF0aXZlX2Fkb3B0X2NvdW50KAogICAgICByZGlmZm5ldCgKICAgICAgICBzZWVkLmdyYXBoID0gbmV0LAogICAgICAgIHQgPSAxMCwKICAgICAgICB0aHJlc2hvbGQuZGlzdCA9IHNhbXBsZSgxOjIsIDUwMEwsIFRSVUUpLAogICAgICAgIHNlZWQubm9kZXMgPSAicmFuZG9tIiwKICAgICAgICBzZWVkLnAuYWRvcHQgPSAuMTAsCiAgICAgICAgZXhwb3N1cmUuYXJncyA9IGxpc3Qob3V0Z29pbmcgPSBGQUxTRSwgbm9ybWFsaXplZCA9IEZBTFNFKSwKICAgICAgICByZXdpcmUgPSBGQUxTRQogICAgICAgICkKICAgICAgKQogIAogICMgQXJlIHdlIHRoZXJlIHlldD8KICBpZiAoIShpICUlIDUwKSkKICAgIG1lc3NhZ2UoIlNpbXVsYXRpb24gIiwgaSwiIG9mICIsIG5zaW0sICIgZG9uZS4iKQp9CgojIEV4dHJhY3RpbmcgcHJvcAphbnNfMWFuZDIgPC0gZG8uY2FsbChyYmluZCwgbGFwcGx5KGFuc18xYW5kMiwgIlsiLCBpPSJwcm9wIiwgaj0pKQoKYW5zXzJhbmQzIDwtIHZlY3RvcigibGlzdCIsIG5zaW0pCnNldC5zZWVkKDIyMykKZm9yIChpIGluIDE6bnNpbSkgewogICMgV2UganVzdCB3YW50IHRoZSBjdW0gYWRvcHQgY291bnQKICBhbnNfMmFuZDNbW2ldXSA8LSAKICAgIGN1bXVsYXRpdmVfYWRvcHRfY291bnQoCiAgICAgIHJkaWZmbmV0KAogICAgICAgIHNlZWQuZ3JhcGggPSBuZXQsCiAgICAgICAgdCA9IDEwLAogICAgICAgIHRocmVzaG9sZC5kaXN0ID0gc2FtcGxlKDI6MywgNTAwTCwgVFJVRSksCiAgICAgICAgc2VlZC5ub2RlcyA9ICJyYW5kb20iLAogICAgICAgIHNlZWQucC5hZG9wdCA9IC4xMCwKICAgICAgICBleHBvc3VyZS5hcmdzID0gbGlzdChvdXRnb2luZyA9IEZBTFNFLCBub3JtYWxpemVkID0gRkFMU0UpLAogICAgICAgIHJld2lyZSA9IEZBTFNFCiAgICAgICAgKQogICAgICApCiAgCiAgIyBBcmUgd2UgdGhlcmUgeWV0PwogIGlmICghKGkgJSUgNTApKQogICAgbWVzc2FnZSgiU2ltdWxhdGlvbiAiLCBpLCIgb2YgIiwgbnNpbSwgIiBkb25lLiIpCn0KCmFuc18yYW5kMyA8LSBkby5jYWxsKHJiaW5kLCBsYXBwbHkoYW5zXzJhbmQzLCAiWyIsIGk9InByb3AiLCBqPSkpCmBgYAoKVGhpcyBjYW4gYWN0dWFsbHkgYmUgc2ltcGxpZmllZCBieSB1c2luZyB0aGUgZnVuY3Rpb24gYHJkaWZmbmV0X211bHRpcGxlYC4gVGhlIGZvbGxvd2luZyBsaW5lcyBvZiBjb2RlIGFjY29tcGxpc2ggdGhlIHNhbWUgYXMgdGhlIHByZXZpb3VzIGNvZGUgYXZvaWRpbmcgdGhlIGZvci1sb29wIChmcm9tIHRoZSB1c2VyJ3MgcGVyc3BlY3RpdmUpLiBCZXNpZGVzIG9mIHRoZSB1c3VhbCBwYXJhbWV0ZXJzIHBhc3NlZCB0byBgcmRpZmZuZXRgLCB0aGUgYHJkaWZmbmV0X211bHRpcGxlYCBmdW5jdGlvbiByZXF1aXJlcyBgUmAgKG51bWJlciBvZiByZXBldGl0aW9ucy9zaW11bGF0aW9ucyksIGFuZCBgc3RhdGlzdGljYCAoYSBmdW5jdGlvbiB0aGF0IHJldHVybnMgdGhlIHN0YXRpc3RpYyBvZiBpbnN0ZXJzdCkuIE9wdGlvbmFsbHksIHRoZSB1c2VyIG1heSBjaG9vc2UgdG8gc3BlY2lmeSB0aGUgbnVtYmVyIG9mIGNsdXN0ZXJzIHRvIHJ1biBpdCBpbiBwYXJhbGxlbCAobXVsdGlwbGUgQ1BVcyk6CgpgYGB7ciByZGlmZm5ldC1tdWx0aXBsZX0KYW5zXzFhbmQzIDwtIHJkaWZmbmV0X211bHRpcGxlKAogICMgTnVtIG9mIHNpbQogIFIgICAgICAgICAgICAgID0gbnNpbSwKICAjIFN0YXRpc3RpYwogIHN0YXRpc3RpYyAgICAgID0gZnVuY3Rpb24oZCkgY3VtdWxhdGl2ZV9hZG9wdF9jb3VudChkKVsicHJvcCIsXSwgCiAgc2VlZC5ncmFwaCAgICAgPSBuZXQsCiAgdCAgICAgICAgICAgICAgPSAxMCwKICB0aHJlc2hvbGQuZGlzdCA9IHNhbXBsZSgxOjMsIDUwMCwgVFJVRSksCiAgc2VlZC5ub2RlcyAgICAgPSAicmFuZG9tIiwKICBzZWVkLnAuYWRvcHQgICA9IC4xLAogIHJld2lyZSAgICAgICAgID0gRkFMU0UsCiAgZXhwb3N1cmUuYXJncyAgPSBsaXN0KG91dGdvaW5nPUZBTFNFLCBub3JtYWxpemVkPUZBTFNFKSwKICAjIFJ1bm5pbmcgb24gNCBjb3JlcwogIG5jcHVzICAgICAgICAgID0gNEwKICApCgpgYGAKCmBgYHtyIHNpbS1zaW0tcmVzdWx0c30KYm94cGxvdChhbnNfMWFuZDIsIGNvbD0iaXZvcnkiLCB4bGFiID0gIlRpbWUiLCB5bGFiID0gIlRocmVzaG9sZCIpCmJveHBsb3QoYW5zXzJhbmQzLCBjb2w9InRvbWF0byIsIGFkZD1UUlVFKQpib3hwbG90KHQoYW5zXzFhbmQzKSwgY29sID0gInN0ZWVsYmx1ZSIsIGFkZD1UUlVFKQpsZWdlbmQoCiAgInRvcGxlZnQiLAogIGZpbGwgPSBjKCJpdm9yeSIsICJ0b21hdG8iLCAic3RlZWxibHVlIiksCiAgbGVnZW5kID0gYygiMS8yIiwgIjIvMyIsICIxLzMiKSwKICB0aXRsZSA9ICJUaHJlc2hvbGQgcmFuZ2UiLAogIGJ0eSA9Im4iCikKYGBgCgoKKiAgIEV4YW1wbGUgc2ltdWxhdGluZyBhIHRob3VzYW5kIG5ldHdvcmtzIGJ5IGNoYW5naW5nIHRocmVzaG9sZCBsZXZlbHMuCiAgICBUaGUgZmluYWwgcHJldmFsZW5jZSwgb3IgaGF6YXJkIGFzIGEgZnVuY3Rpb24gb2YgdGhyZXNob2xkIGxldmVscy4KCiMgUHJvYmxlbXMKCjEuICBHaXZlbiB0aGUgZm9sbG93aW5nIHR5cGVzIG9mIG5ldHdvcmtzOiBTbWFsbC13b3JsZCwgU2NhbGUtZnJlZSwgQmVybm91bGxpLAogICAgd2hhdCBzZXQgb2YgJG4kIGluaXRpYXRvcnMgbWF4aW1pemVzIGRpZmZ1c2lvbj8KICAgICg8YSBocmVmPSJzaW0tc29sdXRpb25zLnIiIHRhcmdldD0iX2JsYW5rIj5zb2x1dGlvbiBzY3JpcHQ8L2E+IGFuZCA8YSBocmVmPSJzaW0tc29sdXRpb25zLnBuZyIgdGFyZ2V0PSJfYmxhbmsiPnNvbHV0aW9uIHBsb3Q8L2E+KQogICAgCgo=
Center for Applied Network Analysis (CANA)