Simulates a diffusion network by creating a random dynamic network and adoption threshold levels.
rdiffnet_multiple(R, statistic, ..., ncpus = 1L, cl = NULL)
rdiffnet(
n,
t,
seed.nodes = "random",
seed.p.adopt = 0.05,
seed.graph = "scale-free",
rgraph.args = list(),
rewire = TRUE,
rewire.args = list(),
threshold.dist = runif(n),
exposure.args = list(),
name = "A diffusion network",
behavior = "Random contagion",
stop.no.diff = TRUE
)Arguments
- R
Integer scalar. Number of simulations to be done.
- statistic
A Function to be applied to each simulated diffusion network.
- ...
Further arguments to be passed to
rdiffnet.- ncpus
Integer scalar. Number of processors to be used (see details).
- cl
An object of class
c("SOCKcluster", "cluster")(see details).- n
Integer scalar. Number of vertices.
- t
Integer scalar. Time length.
- seed.nodes
Either a character scalar or a vector. Type of seed nodes (see details).
- seed.p.adopt
Numeric scalar. Proportion of early adopters.
- seed.graph
Baseline graph used for the simulation (see details).
- rgraph.args
List. Arguments to be passed to rgraph.
- rewire
Logical scalar. When TRUE, network slices are generated by rewiring (see
rewire_graph).- rewire.args
List. Arguments to be passed to
rewire_graph.- threshold.dist
Either a function to be applied via
sapply, a numeric scalar, or a vector/matrix with \(n\) elements. Sets the adoption threshold for each node.- exposure.args
List. Arguments to be passed to
exposure.- name
Character scalar. Passed to
as_diffnet.- behavior
Character scalar. Passed to
as_diffnet.- stop.no.diff
Logical scalar. When
TRUE, the function will return with error if there was no diffusion. Otherwise it throws a warning.
Value
A random diffnet class object.
rdiffnet_multiple returns either a vector or an array depending
on what statistic is (see sapply and
parSapply).
Details
Instead of randomizing whether an individual adopts the innovation or not, this toy model randomizes threshold levels, seed adopters and network structure, so an individual adopts the innovation in time \(T\) iff his exposure is above or equal to his threshold. The simulation is done in the following steps:
Using
seed.graph, a baseline graph is created.Given the baseline graph, the set of initial adopters is defined using
seed.nodes.Afterwards, if
rewire=TRUE\(t-1\) slices of the network are created by iteratively rewiring the baseline graph.The
threshold.distfunction is applied to each node in the graph.Simulation starts at \(t=2\) assigning adopters in each time period accordingly to each vertex's threshold and exposure.
When seed.nodes is a character scalar it can be "marginal", "central" or "random",
So each of these values sets the initial adopters using the vertices with lowest
degree, with highest degree or completely randomly. The number of early adoptes
is set as seed.p.adopt * n. Please note that when marginal nodes are
set as seed it may be the case that no diffusion process is attained as the
chosen set of first adopters can be isolated. Any other case will be considered
as an index (via [<- methods), hence the user can manually set the set of initial adopters, for example
if the user sets seed.nodes=c(1, 4, 7) then nodes 1, 4 and 7 will be
selected as initial adopters.
The argument seed.graph can be either a function that generates a graph
(Any class of accepted graph format (see netdiffuseR-graphs)), a
graph itself or a character scalar in which the user sets the algorithm used to
generate the first network (network in t=1), this can be either "scale-free"
(Barabasi-Albert model using the rgraph_ba function, the default),
"bernoulli" (Erdos-Renyi model using the rgraph_er function),
or "small-world" (Watts-Strogatz model using the rgraph_ws
function). The list rgraph.args passes arguments to the chosen algorithm.
When rewire=TRUE, the networks that follow t=1 will be generated using the
rewire_graph function as \(G(t) = R(G(t-1))\), where \(R\)
is the rewiring algorithm.
If a function, the argument threshold.dist sets the threshold for each vertex in the graph.
It is applied using sapply as follows
sapply(1:n, threshold.dist)By default sets the threshold to be random for each node in the graph.
If seed.graph is provided, no random graph is generated and the simulation
is applied using that graph instead.
rewire.args has the following default options:
p | .1 |
undirected | getOption("diffnet.undirected", FALSE) |
self | getOption("diffnet.self", FALSE) |
exposure.args has the following default options:
outgoing | TRUE |
valued | getOption("diffnet.valued", FALSE) |
normalized | TRUE |
The function rdiffnet_multiple is a wrapper of rdiffnet wich allows
simulating multiple diffusion networks with the same parameters and apply
the same function to all of them. This function is designed to allow the user
to perform larger simulation studies in which the distribution of a particular
statistic is observed.
When cl is provided, then simulations are done via
parSapply. If ncpus is greater than
1, then the function creates a cluster via makeCluster
which is stopped (removed) once the process is complete.
See also
Other simulation functions:
permute_graph(),
rewire_graph(),
rgraph_ba(),
rgraph_er(),
rgraph_ws(),
ring_lattice()
Examples
# Asimple example -----------------------------------------------------------
set.seed(123)
z <- rdiffnet(100,10)
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
z
#> Dynamic network of class -diffnet-
#> Name : A diffusion network
#> Behavior : Random contagion
#> # of nodes : 100 (1, 2, 3, 4, 5, 6, 7, 8, ...)
#> # of time periods : 10 (1 - 10)
#> Type : directed
#> Final prevalence : 0.23
#> Static attributes : real_threshold (1)
#> Dynamic attributes : -
summary(z)
#> Diffusion network summary statistics
#> Name : A diffusion network
#> Behavior : Random contagion
#> -----------------------------------------------------------------------------
#> Period Adopters Cum Adopt. (%) Hazard Rate Density Moran's I (sd)
#> -------- ---------- ---------------- ------------- --------- ----------------
#> 1 5 5 (0.05) - 0.01 -0.02 (0.06)
#> 2 1 6 (0.06) 0.01 0.01 0.09 (0.07)
#> 3 3 9 (0.09) 0.03 0.01 0.32 (0.07) ***
#> 4 2 11 (0.11) 0.02 0.01 0.36 (0.06) ***
#> 5 0 11 (0.11) 0.00 0.01 0.16 (0.07) **
#> 6 3 14 (0.14) 0.03 0.01 0.43 (0.06) ***
#> 7 2 16 (0.16) 0.02 0.01 0.16 (0.06) ***
#> 8 1 17 (0.17) 0.01 0.01 0.14 (0.07) **
#> 9 3 20 (0.20) 0.04 0.01 0.26 (0.07) ***
#> 10 3 23 (0.23) 0.04 0.01 0.36 (0.07) ***
#> -----------------------------------------------------------------------------
#> Left censoring : 0.05 (5)
#> Right centoring : 0.77 (77)
#> # of nodes : 100
#>
#> Moran's I was computed on contemporaneous autocorrelation using 1/geodesic
#> values. Significane levels *** <= .01, ** <= .05, * <= .1.
# A more complex example: Adopt if at least one neighbor has adopted --------
y <- rdiffnet(100, 10, threshold.dist=function(x) 1,
exposure.args=list(valued=FALSE, normalized=FALSE))
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
# Re thinking the Adoption of Tetracycline ----------------------------------
newMI <- rdiffnet(seed.graph = medInnovationsDiffNet$graph,
threshold.dist = threshold(medInnovationsDiffNet), rewire=FALSE)
# Simulation study comparing the diffusion with diff sets of seed nodes -----
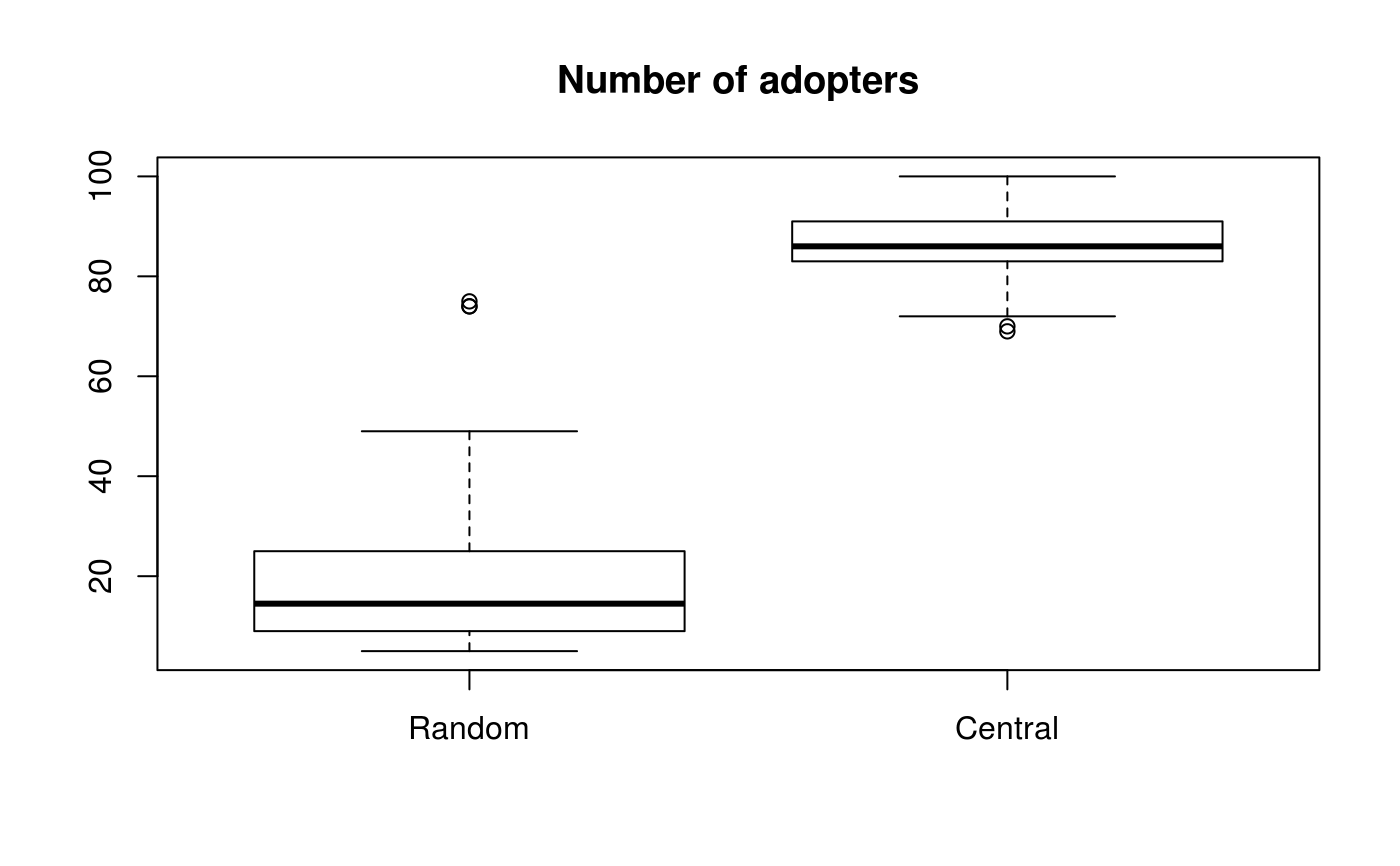
# Random seed nodes
set.seed(1)
ans0 <- rdiffnet_multiple(R=50, statistic=function(x) sum(!is.na(x$toa)),
n = 100, t = 4, seed.nodes = "random", stop.no.diff=FALSE)
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: No diffusion in this network.
# Central seed nodes
set.seed(1)
ans1 <- rdiffnet_multiple(R=50, statistic=function(x) sum(!is.na(x$toa)),
n = 100, t = 4, seed.nodes = "central", stop.no.diff=FALSE)
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
boxplot(cbind(Random = ans0, Central = ans1), main="Number of adopters")