Author

Aníbal Olivera M.

Published

December 6, 2024

New features

#devtools::install_github("USCCANA/netdiffuseR", ref = "47-split-behaviors-rdiffnet")
library(netdiffuseR)

data(kfamily)
kfamily <- subset(kfamily, village %in% c(2, 21))

kfam_diffnet <- survey_to_diffnet(
dat      = kfamily,
idvar    = "id",
netvars  = c("net11", "net12", "net13", "net14", "net15"),
toavar   = "toa",
groupvar = "village"
)

Multiadoption and Disadoption

Some studies aim to analyze the spread of multiple behaviors or innovations within the same setup. Previously, netdiffuseR was unable to handle such data.
There is also significant interest in studying the competition between different behaviors or innovations. For instance, in marketing, simulating the competition between multiple products is highly relevant.
Also, adoption often comes with a boom, but it is usually followed by a decline —riots stop, trends go out of fashion, and exciting gossip becomes old news. So, the adoption of a fashion is followed by the disadoption of that fashion by a new one.
Like theoretical models for adoption —threshold models—, there are some theoretical models for disadoption that could be tested. See, for example, this recent paper.

Starting with version 1.24.0, netdiffuseR supports simulating multi- and dis-adoption diffusion processes.

Multiadoption Simulations

To study a multi-adoption process, you can pass a list as the seed.p.adopt parameter. Here is a simple example:

set.seed(1231)

n <- 200
t <- 10

diffnet_1 <- rdiffnet(
 n, t,
 seed.p.adopt = list(0.1, 0.15)
 )

The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.TRUE

Message: Multi-diffusion behavior simulation selected. Number of behaviors:  2

Message: Object -seed.nodes- converted to a -list-.All behaviors will have the same -random- seed nodes.

Message: Name of 1 behavior provided, but 2 are needed. Names generalized to 'behavior'_1, 'behavior'_2, etc.

diffnet_1

Dynamic network of class -diffnet-
 Name               : A diffusion network
 Behavior           : Random contagion_1, Random contagion_2
 # of nodes         : 200 (1, 2, 3, 4, 5, 6, 7, 8, ...)
 # of time periods  : 10 (1 - 10)
 Type               : directed
 Num of behaviors   : 2
 Prevalence         : 0.29, 0.97
 Static attributes  : real_threshold.1, real_threshold.2 (2)
 Dynamic attributes : -

Inspecting the output from the print method of the diffnet object, we can see that the object contains two behaviors: The “Num of behaviors” entry now shows 2, the “Behavior” entry also shows two behaviors, "Random contagion \_1, Random contagion\_2", and finally, the “Prevalence” entry also shows two numbers: 0.29, 0.97.

Although we are simulating two behaviors, rdiffnet will simulate as many as values are in the seed.p.adopt list.

Tip

In the current implementation of rdiffnet, the multi-adoption module simulates behaviors independently. That is, the code above would be equivalent to simulating the same behavior twice. More complicated models in which behaviors are interdependent are supported via the dis-adoption parameter.

rdiffnet’s defaults will replicate the simulation parameters across behaviors. Nonetheless, we can use lists to specify different parameters for each behavior. For example, the following code simulates two behaviors with different initial adopters, threshold distributions, seed nodes, and labels for the behaviors:

set.seed(1231)

diffnet_2 <- rdiffnet(
 n, t,
 seed.p.adopt = list(0.1, 0.15),
 threshold.dist = list(
   runif(n, .3, .5),
   runif(n, .2, .4)
 ),
 seed.nodes = list("central", "random"),
 behavior   = list("tobacco", "alcohol")
)

diffnet_2

Dynamic network of class -diffnet-
 Name               : A diffusion network
 Behavior           : tobacco, alcohol
 # of nodes         : 200 (1, 2, 3, 4, 5, 6, 7, 8, ...)
 # of time periods  : 10 (1 - 10)
 Type               : directed
 Num of behaviors   : 2
 Prevalence         : 0.98, 0.57
 Static attributes  : real_threshold.1, real_threshold.2 (2)
 Dynamic attributes : -

In this particular example, we ran rdiffnet with most of the parameters being in a list. The reader is invited to look at other types of possible inputs in the rdiffnet documentation.

set.seed(1231)

diffnet_2 <- rdiffnet(
 n, t,
 seed.p.adopt = list(0.1, 0.15),
 threshold.dist = matrix(runif(n * 2, 0.3, 0.5),
                         nrow = n, ncol = 2),
 seed.nodes = c("central", "random"),
 behavior   = c("tobacco", "alcohol")
)

diffnet_2

Dynamic network of class -diffnet-
 Name               : A diffusion network
 Behavior           : tobacco, alcohol
 # of nodes         : 200 (1, 2, 3, 4, 5, 6, 7, 8, ...)
 # of time periods  : 10 (1 - 10)
 Type               : directed
 Num of behaviors   : 2
 Prevalence         : 0.98, 0.57
 Static attributes  : real_threshold.1, real_threshold.2 (2)
 Dynamic attributes : -

As we did in the previous section, we can give a specific network as input.

set.seed(121)

graph <- rgraph_ws(n, t, p=.3)  # Watts-Strogatz model

diffnet_3 <- rdiffnet(
  seed.graph = graph,
  t = t ,
  seed.p.adopt = list(0.1, 0.15)
  )

diffnet_3

Dynamic network of class -diffnet-
 Name               : A diffusion network
 Behavior           : Random contagion_1, Random contagion_2
 # of nodes         : 200 (1, 2, 3, 4, 5, 6, 7, 8, ...)
 # of time periods  : 10 (1 - 10)
 Type               : directed
 Num of behaviors   : 2
 Prevalence         : 0.66, 0.72
 Static attributes  : real_threshold.1, real_threshold.2 (2)
 Dynamic attributes : -

Besides passing fixed networks as we did with the small-world example, the rdiffnet function also supports passing diffnet objects as input. When doing so, the function will use the graph of the diffnet object as the seed graph and will take the time argument as the number of timepoints included in the graph:

set.seed(1231)

diffnet_4 <- rdiffnet(
 seed.graph     = kfam_diffnet,
 seed.p.adopt   = list(0.1, 0.15),
 threshold.dist = runif(nvertices(kfam_diffnet), .3,.5)
 )

diffnet_4

Dynamic network of class -diffnet-
 Name               : A diffusion network
 Behavior           : Random contagion_1, Random contagion_2
 # of nodes         : 113 (1, 2, 3, 4, 5, 6, 7, 8, ...)
 # of time periods  : 11 (1 - 11)
 Type               : directed
 Num of behaviors   : 2
 Prevalence         : 0.73, 0.80
 Static attributes  : real_threshold.1, real_threshold.2 (2)
 Dynamic attributes : -

To visualize the diffusion process when there’s more than one behavior, we can use the split_behaviors function to split the diffnet object into a list of diffnet objects, one for each behavior. Then, we can use the plot_adopters function to visualize the diffusion process for each behavior; moreover, using the par() function in R, we can arrange both plots in a single window:

diffnets <- split_behaviors(diffnet_1)

op <- par(mfrow=c(1,2), cex = .8)

plot_adopters(diffnets[[1]], main = "Behavior 1")
plot_adopters(diffnets[[2]], main = "Behavior 2")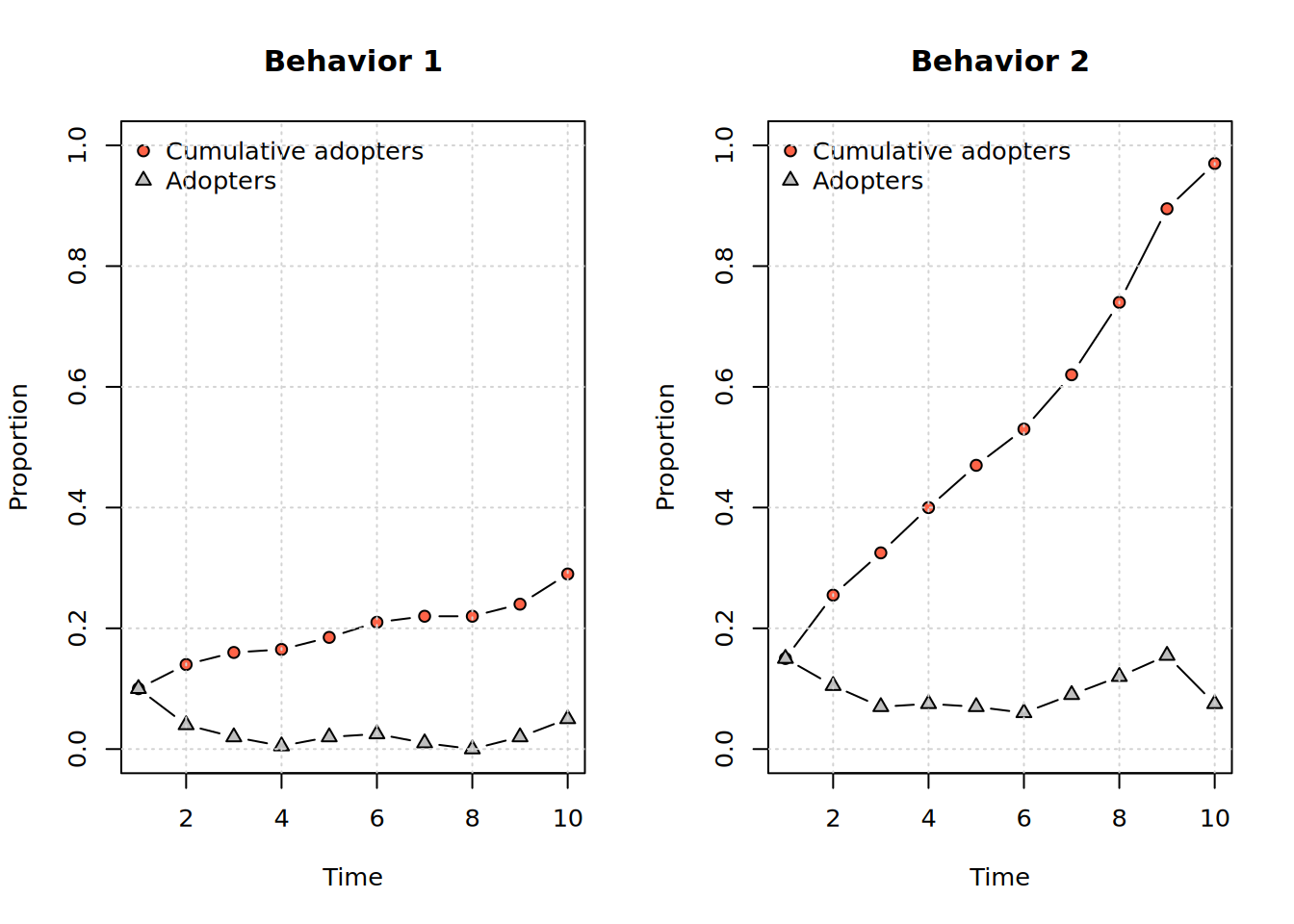

par(op)

Disadoption

The disadoption feature included in netdiffuseR version 1.24.0 opened a new way of studying network diffusion processes. Considering the disadoption of an innovation or behavior is essential for studying significant aspects of competition between products or beliefs (Lehmann 2017 2024. The rdiffnet function includes the disadopt parameter to add a disadoption function, facilitating such analyses and enabling the testing of some theoretical models for disadoption (Alipour 2024).

Some comments about what a disadoption function must be:

It must be a function that receives three arguments: expo, cumadopt, and time.
It must return a list with two elements: the first element is a vector with the nodes that will disadopt, and the second element is a vector with the nodes that will adopt.
If there are no nodes to disadopt or adopt, the function must return an empty vector (integer()).

A template for a disadoption function, which currently returns no disadoption, follows:

disadoption_function <- function(expo, cumadopt, time) {
  list(integer(), integer())
}

The following code shows how to build a disadoption function that randomly selects 10% of the adopters at time t - 1:

random_dis <- function(expo, cumadopt, time) {

 # Number of behaviors
 num_of_behaviors <- dim(cumadopt)[3]
 
 # Making room for the disadopted nodes
 list_disadopt <- list(integer(), integer())
 
 # We iterate through the behaviors
 for (q in 1:num_of_behaviors) {

   # Identifying the adopters at time t-1
   adopters_old <- which(cumadopt[, time - 1, q] == 1)

   if (length(adopters_old) != 0) {

     # selecting 10% of adopters to disadopt
     list_disadopt[[q]] <- sample(
       adopters_old,
       ceiling(0.10 * length(adopters_old)
       )
     )
   }

 }
 return(list_disadopt)
}

It is worth highlighting a few things from the code:

The expo argument is the entire exposure array. This means that it has three dimensions: the first dimension is the number of nodes, the second is the number of time points, and the third is the number of behaviors.
The cumadopt argument is the cumulative adoption array. It has the same dimensions as expo. The value of cumadopt[i, t, q] is 1 if node i has adopted behavior q at time t.
The time argument is the current time point in the simulation. This allows the function to know when the disadopt function is being called.
The code which(cumadopt[, time - 1, q, drop=FALSE] == 1) identifies which nodes had the entry cumadopt equal to 1 at time t - 1.

To simulate a diffusion process with disadoption, we can use the rdiffnet function as follows:

diffnet_5  <- rdiffnet(
 seed.graph   = graph,
 t            = t,
 seed.p.adopt = 0.1,
 disadopt     = random_dis
 )

diffnet_5

Dynamic network of class -diffnet-
 Name               : A diffusion network
 Behavior           : Random contagion
 # of nodes         : 200 (1, 2, 3, 4, 5, 6, 7, 8, ...)
 # of time periods  : 10 (1 - 10)
 Type               : directed
 Num of behaviors   : 1
 Final prevalence   : 0.34
 Static attributes  : real_threshold (1)
 Dynamic attributes : -

Now, using the disadopt function we can build more complex models featuring competing behaviors. For instance, we can build a disadoption function that restricts nodes from adopting more than one behavior at a time, particularly, we can implement the following rule for adopters of behavior 1:

$\text{Disadopt_1}_{it} = \left\{\begin{array}{l}Yes,\quad\text{if behavior 2 has adopted}\\\text{No},\quad\text{otherwise.}\end{array}\right.$

The following code shows how to build such a function:

one_only <- function(expo, cumadopt, time) {

 # Id double adopters
 ids <- which(apply(cumadopt[, time,], 1, sum) == 2)

 # If there are no adopters
 if (length(ids) == 0)
   return(list(integer(), integer()))

 # Otherwise, make them pick one (in this case, we prefer the second)
 return(list(ids, integer()))
}

Of the code above, we can highlight the following:

We are identifying individuals adopting more than one behavior at time t using the code apply(cumadopt[, time,], 1, sum) > 1. In a two behavior model, this will return a vector with values 0 (no adoption), 1 (only one behavior adopted), or 2 (both behaviors adopted).
The which function is used to identify the nodes adopting both behaviors (after calling apply).
If there are no double adopters, the function returns an empty list.

Let’s simulate a diffusion process with the disadoption function one_only:

set.seed(331)

diffnet_6 <- rdiffnet(
 200, 10,
 disadopt = one_only,
 seed.p.adopt = list(0.1, 0.1)
 )

diffnet_6

Dynamic network of class -diffnet-
 Name               : A diffusion network
 Behavior           : Random contagion_1, Random contagion_2
 # of nodes         : 200 (1, 2, 3, 4, 5, 6, 7, 8, ...)
 # of time periods  : 10 (1 - 10)
 Type               : directed
 Num of behaviors   : 2
 Prevalence         : 0.28, 0.42
 Static attributes  : real_threshold.1, real_threshold.2 (2)
 Dynamic attributes : -

To finalize, we can demonstrate that nodes adopted a single behavior by taking the cumulative adoption matrix at the last time point and checking if there are any nodes adopting both behaviors.

We will use the toa_mat function which extract the cumulative adoption matrix from the model:

toas <- toa_mat(diffnet_6)

# Putting the two behaviors together
adopted <-  cbind(
 toas[[1]]$cumadopt[, 10],
 toas[[2]]$cumadopt[, 10]
)

# Looking at the first 5 nodes
head(adopted, 5)

  [,1] [,2]
1    0    0
2    0    1
3    1    0
4    1    0
5    0    1

# Tabulating side by side
table(adopted[, 1], adopted[, 2])

As expected, there’s no entry in the table in which both behaviors were adopted by the same node. Using the disadopt function, we can build (and study) increasingly complex models of network diffusion.

Exercise

Using the template for a disadoption function,

disadoption_function <- function(expo, cumadopt, time) {
  
  # Some fancy calculations..
  
  return(list(integer(), integer()))
}

creates a disadoption function that simulates a fashion that dies incrementally over time. You can try this for one or more fads. (solution file)