Test whether or not a network estimates can be considered structurally dependent, i.e. a function of the network structure. By rewiring the graph and calculating a particular statistic \(t\), the test compares the observed mean of \(t\) against the empirical distribution of it obtained from rewiring the network.
n_rewires(graph, p = c(20L, rep(0.1, nslices(graph) - 1)))
struct_test(graph, statistic, R, rewire.args = list(), ...)
# S3 method for class 'diffnet_struct_test'
c(..., recursive = FALSE)
# S3 method for class 'diffnet_struct_test'
print(x, ...)
# S3 method for class 'diffnet_struct_test'
hist(
x,
main = "Empirical Distribution of Statistic",
xlab = expression(Values ~ of ~ t),
breaks = 20,
annotated = TRUE,
b0 = expression(atop(plain("") %up% plain("")), t[0]),
b = expression(atop(plain("") %up% plain("")), t[]),
ask = TRUE,
...
)
struct_test_asymp(graph, Y, statistic_name = "distance", p = 2, ...)Arguments
- graph
A
diffnetgraph.- p
Either a Numeric scalar or vector of length
nslices(graph)-1with the number of rewires per links.- statistic
A function that returns either a scalar or a vector.
- R
Integer scalar. Number of repetitions.
- rewire.args
List. Arguments to be passed to
rewire_graph- ...
Further arguments passed to the method (see details).
- recursive
Ignored
- x
A
diffnet_struct_testclass object.- main
Character scalar. Title of the histogram.
- xlab
Character scalar. x-axis label.
- breaks
Passed to
hist.- annotated
Logical scalar. When TRUE marks the observed data average and the simulated data average.
- b0
Character scalar. When
annotated=TRUE, label for the value ofb0.- b
Character scalar. When
annotated=TRUE, label for the value ofb.- ask
Logical scalar. When
TRUE, asks the user to type<Enter>to see each plot (as many as statistics where computed).- Y
Numeric vector of length \(n\).
- statistic_name
Character scalar. Name of the metric to compute. Currently this can be either
"distance",">","<","==",">=", or"<=".
Value
A list of class diffnet_struct_test containing the following:
- graph
The graph passed to
struct_test.- p.value
The resulting p-value of the test (see details).
- t0
The observed value of the statistic.
- mean_t
The average value of the statistic applied to the simulated networks.
- R
Number of simulations.
- statistic
The function
statisticpassed tostruct_test.- boot
A
bootclass object as return from the call toboot.- rewire.args
The list
rewire.argspassed tostruct_test.
Details
struct_test computes the test by generating the null distribution using
Monte Carlo simulations (rewiring). struct_test_asymp computes the
test using an asymptotic approximation. While available, we do not recommend
using the asymptotic approximation since it has not shown good results when
compared to the MC approximation. Furthermore, the asymptotic version has only
been implemented for graph as static graph.
The output from the hist method is the same as hist.default.
struct_test is a wrapper for the function boot from the
boot package. Instead of resampling data–vertices or edges–in each iteration the function
rewires the original graph using rewire_graph and applies
the function defined by the user in statistic.
The default values to rewire_graph via rewire.args are:
p | Number or Integer with default n_rewires(graph). |
undirected | Logical scalar with default getOption("diffnet.undirected", FALSE). |
copy.first | Logical scalar with TRUE. |
algorithm | Character scalar with default "swap". |
In struct_test ... are passed to boot, otherwise are passed
to the corresponding method (hist for instance).
From the print method, p-value for the null of the statistic been
equal between graph and its rewired versions is computed as follows
$$% p(\tau)=2\times\min\left(\mbox{Pr}(t\leq\tau), \mbox{Pr}(t\geq\tau)\right) % $$
Where \(\mbox{Pr}\{\cdot\}\) is approximated using the Empirical Distribution Function retrieved from the simulations.
For the case of the asymptotic approximation, under the null we have
$$% \sqrt{n}\left(\hat\beta(Y,G)-\mu_\beta\right)\sim^d\mbox{N}\left(0,\sigma_\beta^2\right) $$
The test is actually on development by Vega Yon and Valente. A copy of the working paper can be distributed upon request to g.vegayon@gmail.com.
The function n_rewires proposes a vector of number of rewirings that
are performed in each iteration.
References
Vega Yon, George G. and Valente, Thomas W. (On development).
Davidson, R., & MacKinnon, J. G. (2004). Econometric Theory and Methods. New York: Oxford University Press.
Examples
# Creating a random graph
set.seed(881)
diffnet <- rdiffnet(100, 5, seed.graph="small-world")
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
# Testing structure-dependency of threshold
res <- struct_test(
diffnet,
function(g) mean(threshold(g), na.rm=TRUE),
R=100
)
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
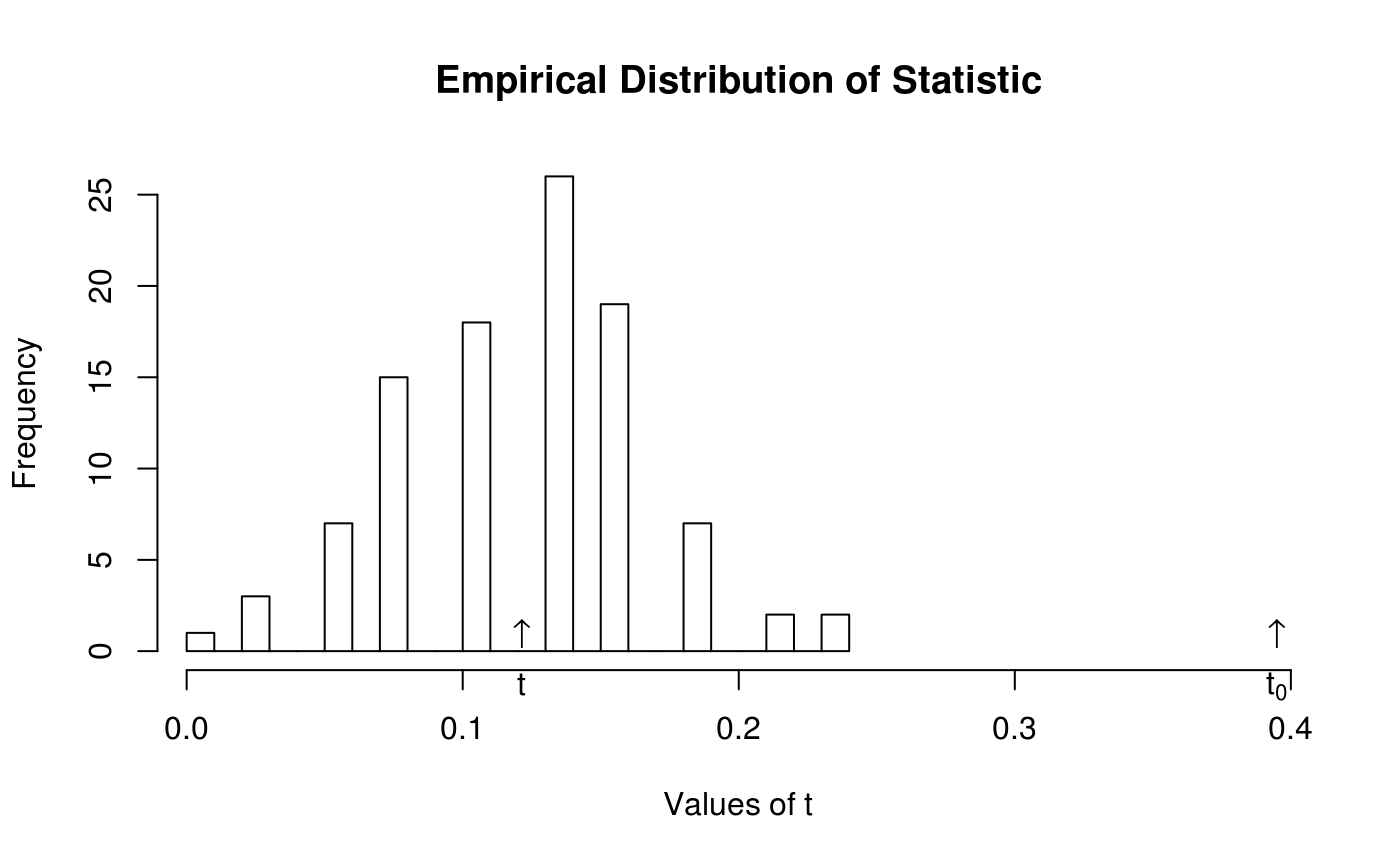
res
#>
#> Structure dependence test
#> # Simulations : 100
#> # nodes : 100
#> # of time periods : 5
#> --------------------------------------------------------------------------------
#> H0: E[beta(Y,G)|G] - E[beta(Y,G)] = 0 (no structure dependency)
#> observed expected p.val
#> 0.3947 0.1261 0.0000
hist(res)
# Adding a legend
legend("topright", bty="n",
legend=c(
expression(t[0]:~Baseline),
expression(t:~Rewired~average)
)
)
 # Concatenating results
c(res, res)
#>
#> Structure dependence test
#> # Simulations : 200
#> # nodes : 100
#> # of time periods : 5
#> --------------------------------------------------------------------------------
#> H0: E[beta(Y,G)|G] - E[beta(Y,G)] = 0 (no structure dependency)
#> observed expected p.val
#> 0.3947 0.1261 0.0000
# Running in parallel fashion
res <- struct_test(
diffnet, function(g) mean(threshold(g), na.rm=TRUE),
R=100, ncpus=2, parallel="multicore"
)
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
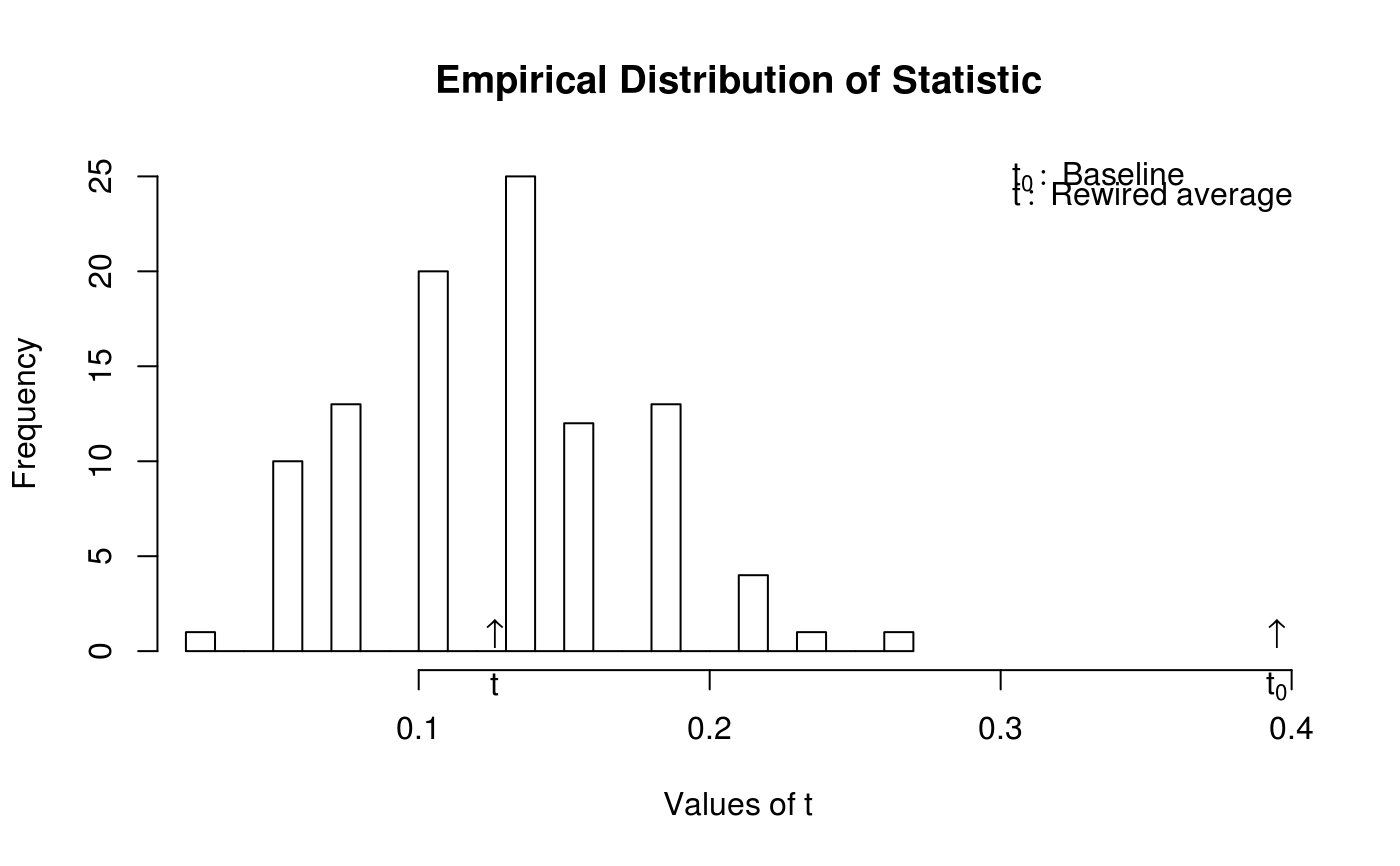
res
#>
#> Structure dependence test
#> # Simulations : 100
#> # nodes : 100
#> # of time periods : 5
#> --------------------------------------------------------------------------------
#> H0: E[beta(Y,G)|G] - E[beta(Y,G)] = 0 (no structure dependency)
#> observed expected p.val
#> 0.3947 0.1158 0.0000
hist(res)
# Concatenating results
c(res, res)
#>
#> Structure dependence test
#> # Simulations : 200
#> # nodes : 100
#> # of time periods : 5
#> --------------------------------------------------------------------------------
#> H0: E[beta(Y,G)|G] - E[beta(Y,G)] = 0 (no structure dependency)
#> observed expected p.val
#> 0.3947 0.1261 0.0000
# Running in parallel fashion
res <- struct_test(
diffnet, function(g) mean(threshold(g), na.rm=TRUE),
R=100, ncpus=2, parallel="multicore"
)
#> Warning: The option -copy.first- is set to TRUE. In this case, the first graph will be treated as a baseline, and thus, networks after T=1 will be replaced with T-1.
res
#>
#> Structure dependence test
#> # Simulations : 100
#> # nodes : 100
#> # of time periods : 5
#> --------------------------------------------------------------------------------
#> H0: E[beta(Y,G)|G] - E[beta(Y,G)] = 0 (no structure dependency)
#> observed expected p.val
#> 0.3947 0.1158 0.0000
hist(res)