Simulation of diffusion networks: rdiffnet

Authors

George G. Vega Yon

Aníbal Olivera M.

Published

June 24, 2025

Modified

June 24, 2025

Recap

Network thresholds (Valente, 1995; 1996), \(\tau\), are defined as the required proportion or number of neighbors that leads you to adopt a particular behavior (innovation), \(a=1\). So, in simulations, the adoption rule follows

\[ a_i = \left\{\begin{array}{ll} 1 &\mbox{if } \tau_i\leq E_i \\ 0 & \mbox{Otherwise} \end{array}\right. ,\qquad \text{where} \quad E_i \equiv \frac{\sum_{j\neq i}\mathbf{X}_{ij}a_j}{\sum_{j\neq i}\mathbf{X}_{ij}}. \]

Where \(E_i\) is i’s exposure to the innovation and \(\mathbf{X}\) is the adjacency matrix (the network).

Here is a review of the concepts we will be using:

  1. Exposure \(E_i\) : Proportion/number of neighbors that has adopted an innovation at each point in time.
  2. Threshold \(\tau\) : The proportion/number of your neighbors who had adopted at or one time period before ego (the focal individual) adopted.
  3. Infectiousness: How much \(i\)’s adoption affects her alters.
  4. Susceptibility: How much \(i\)’s alters’ adoption affects her.
  5. Structural equivalence: How similar are \(i\) and \(j\) in terms of position in the network.

Simulating diffusion networks

We will simulate a diffusion network with the following parameters, using the rdiffnet function included in the package::

  1. Will have 1,000 vertices,
  2. Will span 20 time periods,
  3. The initial adopters (seeds) will be selected random,
  4. Seeds will be a 10% of the network,
  5. The graph (network) will be small-world,
  6. Will use the WS algorithmwith \(p=.2\) (probability of rewire).
  7. Threshold levels will be uniformly distributed between [0.3, 0.7]
# Setting the seed for the RNG
set.seed(1213)

# Generating a random diffusion network
net <- rdiffnet(
  n              = 1e3,                         # 1.
  t              = 20,                          # 2.
  seed.nodes     = "random",                    # 3.
  seed.p.adopt   = .1,                          # 4.
  seed.graph     = "small-world",               # 5.
  rgraph.args    = list(p=.2),                  # 6.
  threshold.dist = function(x) runif(1, .3, .7) # 7.
  )

  • Main features of rdiffnet:

    1. Generatting complex graphs or using your own,

    2. Setting threshold levels per node,

    3. Network rewiring throughout the simulation, and

    4. Setting the seed nodes.

  • The simulation algorithm is as follows:

    1. If required, a baseline graph is created,

    2. Set of initial adopters and threshold distribution are established,

    3. The set of t networks is created (if required), and

    4. Simulation starts at t=2, assigning adopters based on exposures and thresholds:

      1. For each \(i \in N\), if its exposure at \(t-1\) is greater than its threshold, then adopts, otherwise continue without change.

      2. next \(i\)

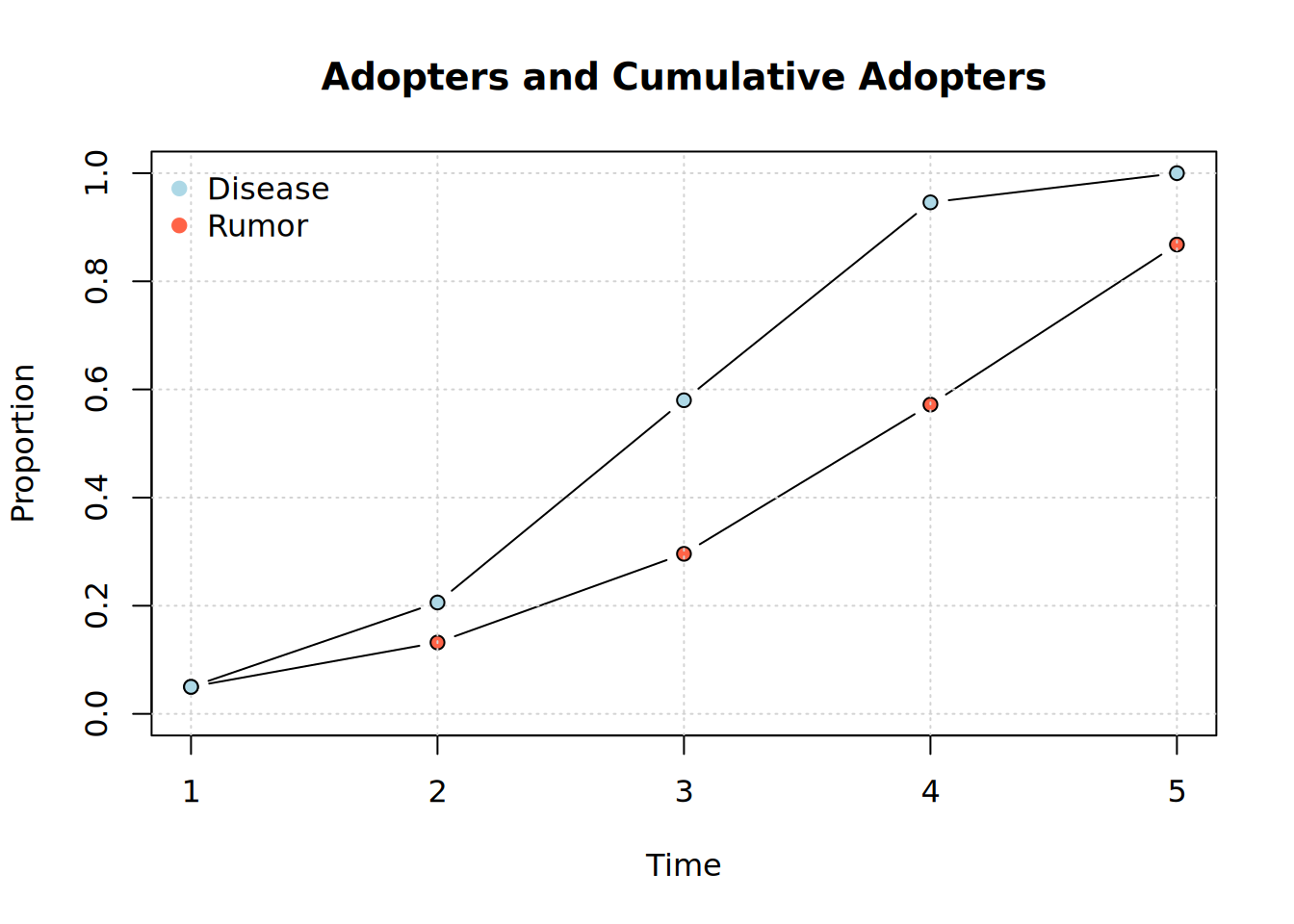
Rumor spreading vs Disease

library(netdiffuseR)

set.seed(09)
diffnet_disease <- rdiffnet(
  n = 5e2,
  t = 5, 
  seed.graph = "small-world",
  rgraph.args = list(k = 4, p = .3),
  seed.nodes = "random",
  seed.p.adopt = .05,
  rewire = TRUE,
  threshold.dist = function(i) 1L,
  exposure.args = list(normalized = FALSE),
  name = "Disease spreading"
  )

diffnet_rumor <- rdiffnet(
  seed.graph = diffnet_disease$graph,
  seed.nodes = which(diffnet_disease$toa == 1),
  rewire = FALSE,
  threshold.dist = function(i) rbeta(1, 3, 10),
  name = "Rumor spreading",
  behavior = "Some rumor"
)

plot_adopters(diffnet_rumor, what = "cumadopt", include.legend = FALSE)
plot_adopters(diffnet_disease, bg="lightblue", add=TRUE, what = "cumadopt")
legend(
  "topleft",
  legend = c("Disease", "Rumor"),
  col = c("lightblue", "tomato"),
  bty = "n", pch=19
  )

Problems

  1. Using the Korean family village 21, compare which strategy setting the seed nodes maximizes the diffusion. Use rdiffnet_multiple to run 500 simulations for each strategy. The strategies are:

    • Random seed nodes.
    • Central seed nodes.
    • Marginal seed nodes.
    • One of your own making.

(solution script and solution plot)

  1. Given the following types of networks: Small-world, Scale-free, Bernoulli, what set of \(n\) initiators maximizes diffusion? (solution script and solution plot)

Appendix

Not using rdiffnet_multiple

The following is example code that can be used to run multiple simulations like it is done using the rdiffnet_multiple function. We do not recommend this approach but it may be useful for some users:

# Now, simulating a bunch of diffusion processes
nsim <- 500L
ans_1and2 <- vector("list", nsim)
set.seed(223)
for (i in 1:nsim) {
  # We just want the cum adopt count
  ans_1and2[[i]] <- 
    cumulative_adopt_count(
      rdiffnet(
        seed.graph = net,
        threshold.dist = sample(1:2, 1000L, TRUE),
        seed.nodes = "random",
        seed.p.adopt = .10,
        exposure.args = list(outgoing = FALSE, normalized = FALSE),
        rewire = FALSE
        )
      )
  
  # Are we there yet?
  if (!(i %% 50))
    message("Simulation ", i," of ", nsim, " done.")
}
# Simulation 50 of 500 done.
# Simulation 100 of 500 done.
# Simulation 150 of 500 done.
# Simulation 200 of 500 done.
# Simulation 250 of 500 done.
# Simulation 300 of 500 done.
# Simulation 350 of 500 done.
# Simulation 400 of 500 done.
# Simulation 450 of 500 done.
# Simulation 500 of 500 done.
# Extracting prop
ans_1and2 <- do.call(rbind, lapply(ans_1and2, "[", i="prop", j=))

ans_2and3 <- vector("list", nsim)
set.seed(223)
for (i in 1:nsim) {
  # We just want the cum adopt count
  ans_2and3[[i]] <- 
    cumulative_adopt_count(
      rdiffnet(
        seed.graph = net,
        threshold.dist = sample(2:3, 1000L, TRUE),
        seed.nodes = "random",
        seed.p.adopt = .10,
        exposure.args = list(outgoing = FALSE, normalized = FALSE),
        rewire = FALSE
        )
      )
  
  # Are we there yet?
  if (!(i %% 50))
    message("Simulation ", i," of ", nsim, " done.")
}
# Simulation 50 of 500 done.
# Simulation 100 of 500 done.
# Simulation 150 of 500 done.
# Simulation 200 of 500 done.
# Simulation 250 of 500 done.
# Simulation 300 of 500 done.
# Simulation 350 of 500 done.
# Simulation 400 of 500 done.
# Simulation 450 of 500 done.
# Simulation 500 of 500 done.
ans_2and3 <- do.call(rbind, lapply(ans_2and3, "[", i="prop", j=))

Example by changing threshold (rdiffnet_multiple)

The following block of code runs multiple diffnet simulations.

Before we proceed, we will generate a scale-free homophilic network using rgraph_ba:

# Simulating a scale-free homophilic network
set.seed(1231)
X <- rep(c(1,1,1,1,1,0,0,0,0,0), 50)

net <- rgraph_ba(t = 499, m=4, eta = X)

# Taking a look in igraph
ig  <- igraph::graph_from_adjacency_matrix(net)
plot(ig, vertex.color = c("azure", "tomato")[X+1], vertex.label = NA,
     vertex.size = sqrt(dgr(net)))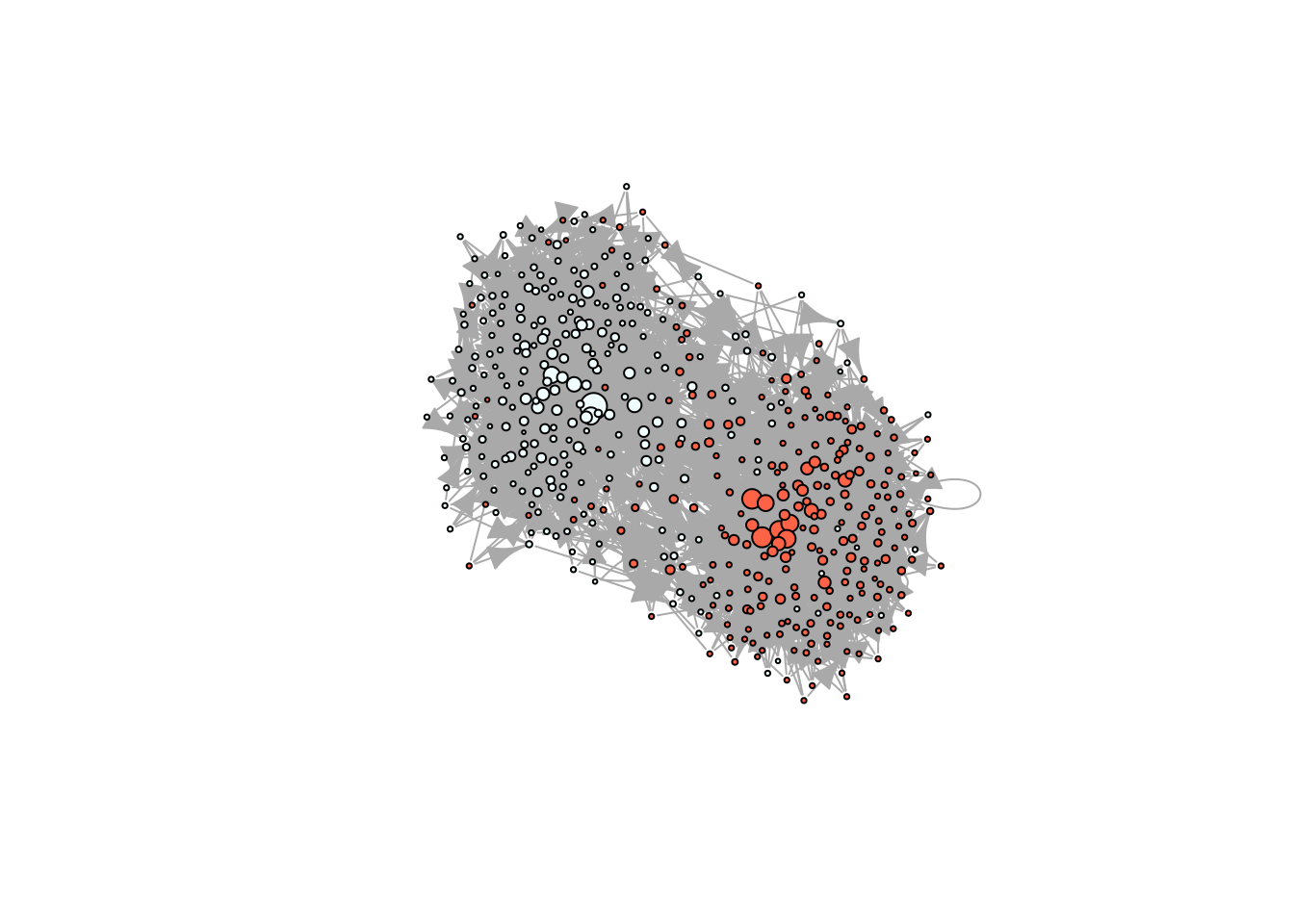

Besides of the usual parameters passed to rdiffnet, the rdiffnet_multiple function requires:

  • R (number of repetitions/simulations), and
  • statistic (a function that returns the statistic of insterst).

Optionally, the user may choose to specify the number of clusters to run it in parallel (multiple CPUs):

nsim <- 500L

ans_1and2 <- rdiffnet_multiple(
  # Num of sim
  R              = nsim,
  # Statistic
  statistic      = function(d) cumulative_adopt_count(d)["prop",], 
  seed.graph     = net,
  t              = 10,
  threshold.dist = sample(1:2, 500L, TRUE),
  seed.nodes     = "random",
  seed.p.adopt   = .1,
  rewire         = FALSE,
  exposure.args  = list(outgoing=FALSE, normalized=FALSE),
  # Running on 4 cores
  ncpus          = 4L
  ) |> t()

ans_2and3 <- rdiffnet_multiple(
  # Num of sim
  R              = nsim,
  # Statistic
  statistic      = function(d) cumulative_adopt_count(d)["prop",], 
  seed.graph     = net,
  t              = 10,
  threshold.dist = sample(2:3, 500, TRUE),
  seed.nodes     = "random",
  seed.p.adopt   = .1,
  rewire         = FALSE,
  exposure.args  = list(outgoing=FALSE, normalized=FALSE),
  # Running on 4 cores
  ncpus          = 4L
  ) |> t()

ans_1and3 <- rdiffnet_multiple(
  # Num of sim
  R              = nsim,
  # Statistic
  statistic      = function(d) cumulative_adopt_count(d)["prop",], 
  seed.graph     = net,
  t              = 10,
  threshold.dist = sample(1:3, 500, TRUE),
  seed.nodes     = "random",
  seed.p.adopt   = .1,
  rewire         = FALSE,
  exposure.args  = list(outgoing=FALSE, normalized=FALSE),
  # Running on 4 cores
  ncpus          = 4L
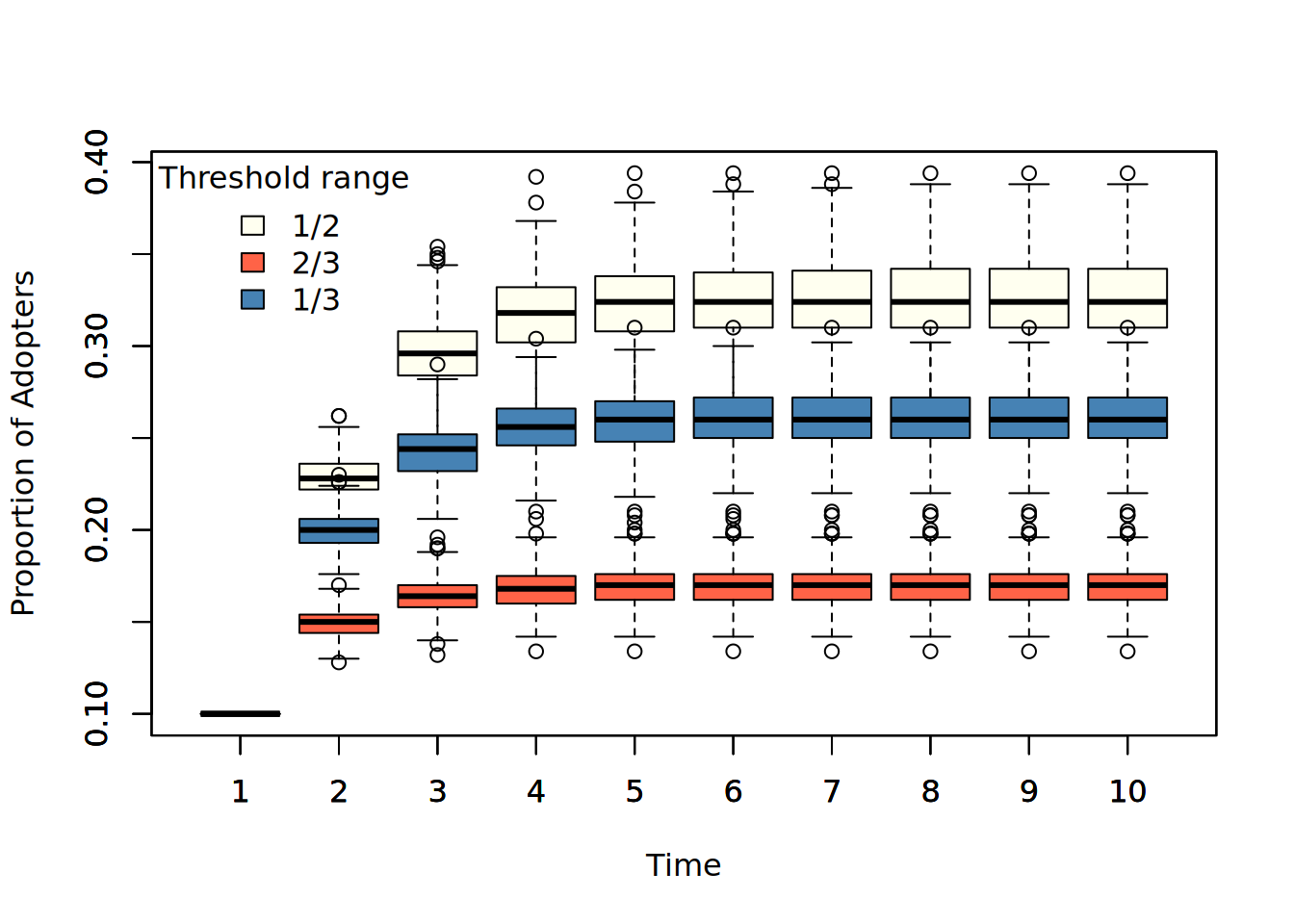
  ) |> t()
  • By simulating 1000 times each diffusion, we can see the final prevalence is a function of threshold levels.
boxplot(ans_1and2, col="ivory", xlab = "Time", ylab = "Proportion of Adopters")
boxplot(ans_2and3, col="tomato", add=TRUE)
boxplot(ans_1and3, col = "steelblue", add=TRUE)
legend(
  "topleft",
  fill = c("ivory", "tomato", "steelblue"),
  legend = c("1/2", "2/3", "1/3"),
  title = "Threshold range",
  bty ="n"
)